Stress/displacement model change: static | ||
| ||
ProductsAbaqus/Standard
Elements tested
- C3D8
- C3D8I
- C3D8R
- CAX4H
- CGAX3HT
- CGAX4HT
- CGAX4RH
- CGAX6M
- CGAX6MH
- CGAX8HT
- CGAX8RHT
- CPE4
- CPE4I
- CPE4R
- CPE4RT
- CPE4RHT
- CPE8
- CPS4
- CPS4R
- CPS4RT
- CPEG4RT
- CPEG4RHT
- CPEG6M
- CPEG6MH
- DCOUP2D
- S4
- SC8R
- SC6R
- T2D2
- CSS8
![]()
Features tested
Continuum stress/displacement elements are removed and added during a static analysis. General nonlinear and linear perturbation steps are tested with elastic, hyperelastic, and plastic material properties. Various modeling features, such as multi-point constraints and transformed nodal and element variables, are tested in conjunction with element removal/reactivation.
![]()
Problem description
Model:
All models have dimensions 5.0 × 2.0 in the x–y plane, with an out-of-plane dimension of 1.0 (plane stress/strain analysis). The axisymmetric models are 5.0 units in the z-direction and have an inner radius of 1.0 units.
Material:
The material is assumed to be a compressible rubber, except in the elastic-plastic test. The material constants are not given in any specific set of units. The rubber is modeled both as a hyperelastic material and as a linear elastic material that matches the hyperelastic material at small strain.
- Elastic material:
-
Young's modulus = 4.064385 × 106
Poisson's ratio = 0.451566
- Hyperelastic material:
-
= 56.00 × 104
= 14.00 × 104
= 1.43 × 10−7
- Elastic-plastic material:
-
Young's modulus = 3.0 × 106
Poisson's ratio = 0.3
Plastic hardening:
Yield stress Plastic strain 0.15 × 105 0.0000 0.60 × 105 2.027 × 10−4
Loading and boundary conditions
- General tests:
-
The loading in Step 1 is to compress the right-hand side of the model 0.1 units in the x-direction, while the left-hand side is fixed in the x-direction. In Step 2 the middle portion of the model, consisting of elements 2–4 and 7–9, is removed (see Figure 1). This releases the load in the remaining elements. In Step 3 the nodes of the removed elements are repositioned to their original positions in the y- and, if applicable, z-directions. In Step 4 the elements are added back into the model and the right-hand side nodes are displaced to the position x = 5.1, corresponding to a displacement of 0.1 units. The loading for the axisymmetric models is in the z-direction.
Figure 1. Mesh used in general static tests.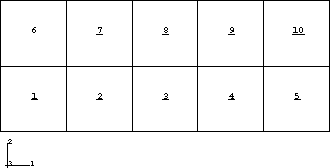
- Specific tests:
-
The loading for the specific tests is identical to that used in the general tests with the following exceptions: pmce_cpe8_se1.inp and pmce_cpe8_sh1.inp, which have body loads active during all steps of the analysis; pmce_c3d8_se1.inp, which has a predefined temperature load but no displacement boundary condition (except to constrain rigid body motion); pmce_cpe4i_se1.inp, in which prescribed displacements are 10−2 times those of the other tests; and pmce_cpe4_sp.inp and pmce_cpe4_sp1.inp, where the displacement in the fourth step is such that only the newly introduced elements yield.
- pmce_c3d8_se1.inp
-
The initial temperature is = 20. The middle portion of the model is removed in Step 1. In Step 2 the temperature at the nodes of the removed elements is reset to = 100. In Step 3 the nodal temperatures of the removed elements are set to = 180, and the temperatures at the other nodes in the model are reset to = 60. The coefficient of thermal expansion for the middle elements is one half that of the other elements.
- pmce_cpe4_sp.inp
-
In Step 4 the right-hand-side nodes are given an x-displacement of = −0.005 so that only the reactivated elements yield in this step (having been annealed, they have not hardened as the other elements have).
- pmce_cpe4_sp1.inp
-
This problem is identical to pmce_cpe4_sp.inp, except that a DCOUP2D element is removed in Step 1 and added in Step 4 to apply the x-displacement of = −0.005.
- pmce_cpe4i_se1.inp
-
The elements have a stiffness 100 times that of the elements in the other tests. Each of the elements has a single line of rebar that runs through the middle of the element parallel to the x-axis. The rebar has 1% of the cross-sectional area of the element at the face it cuts. It is given a stiffness in plane stress that is 100 times the plane strain modulus of the element. This ensures that the rebar exactly doubles the stiffness of the element. This model is verified with small displacements to avoid the effect of thinning of the rebar cross-section as it stretches.
- pmce_cpe8_se1.inp and pmce_cpe8_sh1.inp
-
The body load on each of these models is equal to 70000 units in the x-direction.
![]()
Reference solution
These models (except for pmce_cps4_se1.inp, pmce_cps4r_se1.inp, pmce_cgax4rh_se1.inp, and pmce_c3d8r_se1.inp) include nonlinear geometric terms. This loading regime puts the model in uniaxial stress in the plane stress, axisymmetric, and three-dimensional models; in the plane strain model it is in a biaxial state of stress. Hence, the stress can be found by multiplying the strain by the elastic modulus or, in the case of plane strain, by . Only the strain value will be listed.
- General tests:
-
- Step 1
-
Uniform axial strain should exist in this step for all tests. The value should be ln (), where l = 4.9 and = 5.0. These values give = −2.0203 × 10−2.
- Step 2
-
The stress and strain in the elements that are not removed should become zero. The nodes on elements 1 and 6 should have = 0.0, and the nodes on elements 5 and 10 should have = −0.1.
- Step 3
-
The displacement of the nodes in this step should have no effect on the results that were obtained in Step 2.
- Step 4
-
For the plane strain, axisymmetric, and three-dimensional models there will be a state of uniform axial strain in this step. The magnitude will be = 4.0005 × 10−2 (ln (), where l = 5.1 and = 4.9).
For the plane stress and truss elements there is a change in thickness of the elements in Step 1. The thickness is not changed when elements are removed. Therefore, the elements added back into the model in this step will not have the same axial stiffness (and, hence, axial strain) as the elements that were not removed. The variation in is as follows: elements 1, 5, 6, and 10 have = 4.07 × 10−2; elements 2, 4, 7, and 9 have = 3.92 × 10−2; elements 3 and 8 have = 3.99 × 10−2.
The axisymmetric models are loaded in the z-direction.
- Specific tests:
-
The models that have the same loading as the general tests have the same analytical solution.
- pmce_cps4_se1.inp
-
Because this is a test without NLGEOM, the strain is always based on the change in displacement divided by the original length. This produces = −2 × 10−2 in Step 1 and 4 × 10−2 in Step 4.
- pmce_c3d8_se1.inp
-
There should be zero response in the model in Step 1 and Step 2. In Step 3 there should be thermal strains in the model equal to for the middle elements and for the other elements. (These thermal strains are the same value since the value for the middle elements is one-half of that for the other elements.) There should be no elastic strain in the model and no stress.
- pmce_cpe4_sp.inp and pmce_cpe4_sp1.inp
-
In Step 1 the model will yield uniformly. = −1.879 × 10−4. In Step 4 only the middle elements of the model will yield. will be approximately −1.76 × 10−4.
- pmce_cpe4i_se1.inp
-
The strains in Steps 1 and 4 are = −2 × 10−4 and 4 × 10−4, respectively. This applies to both the rebar and the elements.
- pmce_cpe8_se1.inp and pmce_cpe8_sh1.inp
-
In Step 1 there will be a gradient of in the model. In Step 2 elements 1 and 6 will be in tension and Elements 5 and 10 will be in compression. In Step 4 there will be a gradient of in the model.
![]()
Results and discussion
All models produce results that match the expected theoretical values.
![]()
Input files
General tests
- pmce_c3d8i_se.inp
-
C3D8I elements, elastic material.
- pmce_c3d8i_sh.inp
-
C3D8I elements, hyperelastic material.
- pmce_c3d8r_se.inp
-
C3D8R elements, elastic material.
- pmce_cax4h_se.inp
-
CAX4H elements, elastic material.
- pmce_cax4h_sh.inp
-
CAX4H elements, hyperelastic material.
- pmce_cgax3ht_sh.inp
-
CGAX3HT elements, hyperelastic material.
- pmce_cgax4ht_sh.inp
-
CGAX4HT elements, hyperelastic material.
- pmce_cgax4rh_sh.inp
-
CGAX4RH elements, hyperelastic material.
- pmce_cgax6m_sh.inp
-
CGAX6M elements, hyperelastic material.
- pmce_cgax6mh_sh.inp
-
CGAX6MH elements, hyperelastic material.
- pmce_cgax8ht_sh.inp
-
CGAX8HT elements, hyperelastic material.
- pmce_cgax8rht_sh.inp
-
CGAX8RHT elements, hyperelastic material.
- pmce_cpe4r_sh.inp
-
CPE4R elements, hyperelastic material.
- pmce_cpe4rt_se.inp
-
CPE4RT elements, elastic material.
- pmce_cpe4rt_sh.inp
-
CPE4RT elements, hyperelastic material.
- pmce_cpe4rht_se.inp
-
CPE4RHT elements, elastic material.
- pmce_cpe4rht_sh.inp
-
CPE4RHT elements, hyperelastic material.
- pmce_cpeg4rt_se.inp
-
CPEG4RT elements, elastic material.
- pmce_cpeg4rt_sh.inp
-
CPEG4RT elements, hyperelastic material.
- pmce_cpeg4rht_se.inp
-
CPEG4RHT elements, elastic material.
- pmce_cpeg4rht_sh.inp
-
CPEG4RHT elements, hyperelastic material.
- pmce_cpe8_se.inp
-
CPE8 elements, elastic material.
- pmce_cpe8_sh.inp
-
CPE8 elements, hyperelastic material.
- pmce_cps4_se.inp
-
CPS4 elements, elastic material.
- pmce_cps4_sh.inp
-
CPS4 elements, hyperelastic material.
- pmce_cps4rt_se.inp
-
CPS4RT elements, elastic material.
- pmce_cps4rt_sh.inp
-
CPS4RT elements, hyperelastic material.
- pmce_cpeg6m_sh.inp
-
CPEG6M elements, hyperelastic material.
- pmce_cpeg6mh_sh.inp
-
CPEG6MH elements, hyperelastic material.
- pmce_s4_se.inp
-
S4 elements, elastic material.
- pmce_sc8r_se.inp
-
SC8R elements, elastic material.
- pmce_sc6r_se.inp
-
SC6R elements, elastic material.
- pmce_t2d2_se.inp
-
T2D2 elements, elastic material.
- pmce_css8_se.inp
-
CSS8 elements, elastic material.
- pmce_css8_sh.inp
-
CSS8 elements, hyperelastic material.
Specific tests
- pmce_c3d8_se1.inp
-
C3D8 elements with TEMPERATURE.
- pmce_c3d8i_sh1.inp
-
C3D8I elements with TRANSFORM on all nodes.
- pmce_c3d8r_se1.inp
-
C3D8R elements without NLGEOM.
- pmce_cgax4rh_se1.inp
-
CGAX4RH elements without NLGEOM.
- pmce_cpe4_se1.inp
-
CPE4 elements with ORIENTATION.
- pmce_cpe4_sh1.inp
-
CPE4 elements with UHYPER and perturbation step.
- pmce_cpe4_sh1.f
-
User subroutine UHYPER used in pmce_cpe4_sh1.inp.
- pmce_cpe4_sp.inp
-
CPE4 elements with elastic-plastic material.
- pmce_cpe4_sp1.inp
-
CPE4 and DCOUP2D elements with elastic-plastic material.
- pmce_cpe4i_se1.inp
-
CPE4I elements with rebar.
- pmce_cpe8_se1.inp
-
CPE8 elements with GRAV-type DLOAD.
- pmce_cpe8_sh1.inp
-
CPE8 elements with BX-type DLOAD.
- pmce_cps4_se1.inp
-
CPS4 elements without NLGEOM.
- pmce_cps4_sh1.inp
-
CPS4 elements with MPC.
- pmce_cps4r_se1.inp
-
CPS4R elements without NLGEOM.