Postprocessing

Determine the stiffness of the mount by creating an X–Y plot of the displacement of the steel plate as a function of the applied load. You will first create a plot of the vertical displacement of the node on the steel plate for which you wrote data to the output database file. Data were written for the node in set Out in this model.

To create a history curve of vertical displacement and swap the
X- and
Y-axes:

1. In the Results Tree, expand the History Output container underneath the output database named Mount.odb.

2. Locate and select the vertical displacement U2 at the node in set Out.

3. Click mouse button 3, and select Save As from the menu that appears to save the X–Y data.

   The Save XY Data As dialog box appears.

4. In the Save XY Data As dialog box, name the curve SWAPPED and select swap(XY) as the save operation; click OK.

   The plot of time-displacement appears in the viewport.

You now have a curve of time-displacement. What you need is a curve showing force-displacement. This is easy to create because in this simulation the force applied to the mount is directly proportional to the total time in the analysis. All you have to do to plot a force-displacement curve is multiply the curve SWAPPED by the magnitude of the load (5.5 kN).

To multiply a curve by a constant value:

1. In the Results Tree, double-click XYData.

   The Create XY Data dialog box appears.

2. Select Operate on XY data, and click Continue.

   The Operate on XY Data dialog box appears.

3. In the XY Data field, double-click SWAPPED.

   The expression "SWAPPED" appears in the text field at the top of the dialog box. Your cursor should be at the end of the text field.

4. Multiply the data object in the text field by the magnitude of the applied load by entering *5500.

5. Save the multiplied data object by clicking Save As at the bottom of the dialog box.

   The Save XY Data As dialog box appears.

6. In the Name text field, type FORCEDEF; and click OK to close the dialog box.

7. To view the force-displacement plot, click Plot Expression at the bottom of the Operate on XY Data dialog box.

You have now created a curve with the force-deflection characteristic of the mount (the axis labels do not reflect this since you did not change the actual variable plotted). To get the stiffness, you need to differentiate the curve FORCEDEF. You can do this by using the differentiate( ) operator in the Operate on XY Data dialog box.

To obtain the stiffness:

1. In the Operate on XY Data dialog box, clear the current expression.

2. From the Operators listed, click differentiate(X).

   differentiate( ) appears in the text field at the top of the dialog box.

3. In the XY Data field, double-click FORCEDEF.

   The expression differentiate( "FORCEDEF" ) appears in the text field.

4. Save the differentiated data object by clicking Save As at the bottom of the dialog box.

   The Save XY Data As dialog box appears.

5. In the Name text field, type STIFF; and click OK to close the dialog box.

6. To plot the stiffness-displacement curve, click Plot Expression at the bottom of the Operate on XY Data dialog box.

7. Click Cancel to close the dialog box.

8. Open the Axis Options dialog box, and switch to the Title tabbed page.

9. Customize the axis titles so they appear as shown in Figure 1.

   Figure 1. Stiffness characteristic of the mount.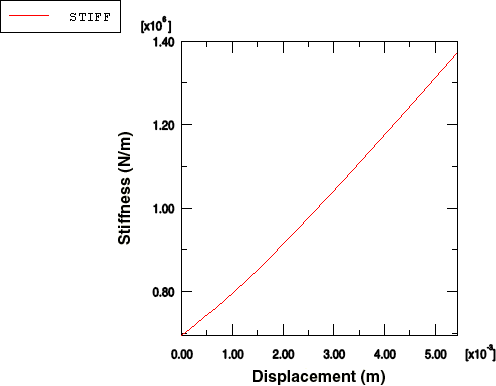
   
   

10. Click Dismiss to close the Axis Options dialog box.

The stiffness of the mount increases by almost 100% as the mount deforms. This is a result of the nonlinear nature of the rubber and the change in shape of the mount as it deforms. Alternatively, you could have created the stiffness-displacement curve directly by combining all the operators above into one expression.

To define the stiffness curve directly:

1. In the Results Tree, double-click XYData.

   The Create XY Data dialog box appears.

2. Select Operate on XY data, and click Continue.

   The Operate on XY Data dialog box appears.

3. From the Operators listed, click differentiate(X).

   differentiate( ) appears in the text field at the top of the dialog box.

4. In the XY Data field, double-click SWAPPED.

   The expression differentiate( "SWAPPED" ) appears in the text field.

5. Place the cursor in the text field directly after the "SWAPPED" data object, and type *5500 to multiply the swapped data by the constant total force value.

   differentiate( "SWAPPED"*5500 ) appears in the text field.

6. Save the differentiated data object by clicking Save As at the bottom of the dialog box.

   The Save XY Data As dialog box appears.

7. In the Name text field, type STIFFNESS; and click OK to close the dialog box.

8. Click Cancel to close the Operate on XY Data dialog box.

9. Customize the X- and Y-axis labels as they appear in Figure 1 if you have not already done so.

10. In the Results Tree, click mouse button 3 on STIFFNESS underneath the XYData container and select Plot from the menu that appears to view the plot in Figure 1 that shows the variation of the mount's axial stiffness as the mount deforms.

You will begin by plotting the undeformed model shape of the mount.

To plot the undeformed model shape:

From the main menu bar, select PlotUndeformed Shape; or use the tool in the Visualization module toolbox to plot the undeformed model shape (see Figure 2).

Figure 2. Undeformed model shape of the rubber mount.

If the figure obscures the plot title, you can move the plot by clicking the tool and holding down mouse button 1 to pan the deformed shape to the desired location. Alternatively, you can turn the plot title off (ViewportViewport Annotation Options).

In this figure the axisymmetric model is displayed as a planar, two-dimensional shape. You can producing a three-dimensional visual effect by sweeping the model through a specified angle. In addition, you can also mirror results about selected planes (such as symmetry planes) to render results on a full three-dimensional representation of the model. These are visualization aids only. Any numerical representation of the results, such as the contour legend, indicates only the portion of the model that was analyzed. Since in this problem the symmetry plane does not necessarily coincide with one of the global coordinate system planes, a local system will be defined to facilitate the mirroring operation.

To define a local coordinate system for
postprocessing:

1. From the main menu bar, select ToolsCoordinate SystemCreate.

2. In the Create Coordinate System dialog box, enter rectangular as the name and click Continue.

3. Select the node at the top-left corner of the model as the origin, the node at the top-right corner as the point on the X-axis, and the node at the bottom-left corner as the point in the X–Y plane.

To mirror and sweep the
cross-section:

1. From the main menu bar, select ViewODB Display Options.

2. In the ODB Display Options dialog box, click the Mirror/Pattern tab.

3. Select rectangular from the Mirror CSYS list.

4. Select XZ as the mirror plane.

5. Click Apply.

   The mirrored image appears.

6. Click the Sweep/Extrude tab.

7. Toggle on Sweep elements and set the sweep range from 0 to 270 degrees. Set the number of segments to 45.

8. Click OK.

   The swept image appears. To more clearly distinguish between the rubber and the steel, color code the model based on section assignment.

You will now plot the deformed model shape of the mount. This will allow you to evaluate the quality of the deformed mesh and to assess the need for mesh refinement.

To plot the deformed model shape:

From the main menu bar, select PlotDeformed Shape, or use the tool to plot the deformed model shape of the mount (see Figure 3).

Figure 3. Deformed model shape of the rubber under an applied load of 5500 N (mirrored/swept image).

The plate has been pushed up, causing the rubber to bulge at the sides. Zoom in on the bottom left corner of the mesh using the tool from the View Manipulation toolbar. Click mouse button 1, and hold it down to define the first corner of the new view; move the mouse to create a box enclosing the viewing area that you want (Figure 4); and release the mouse button. Alternatively, you can zoom and pan the plot by selecting ViewSpecify from the main menu bar.

You should have a plot similar to the one shown in Figure 4 (in this and the images that follow, the sweep and mirroring operations applied earlier have been suppressed).

Figure 4. Distortion at the left-hand corner of the rubber mount model.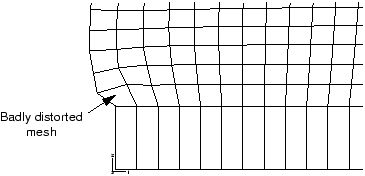

Some elements in this corner of the model are becoming badly distorted because the mesh design in this area was inadequate for the type of deformation that occurs there. Although the shape of the elements is fine at the start of the analysis, they become badly distorted as the rubber bulges outward, especially the element in the corner. If the loading were increased further, the element distortion may become so excessive that the analysis may abort. Mesh design for large distortions discusses how to improve the mesh design for this problem.

The keystoning pattern exhibited by the distorted elements in the bottom right-hand corner of the model indicates that they are locking. A contour plot of the hydrostatic pressure stress in these elements (without averaging across elements sharing common nodes) shows rapid variation in the pressure stress between adjacent elements. This indicates that these elements are suffering from volumetric locking, which was discussed earlier in Selecting elements for elastic-plastic problems, in the context of plastic incompressibility. Volumetric locking arises in this problem from overconstraint. The steel is very stiff compared to the rubber. Thus, along the bond line the rubber elements cannot deform laterally. Since these elements must also satisfy incompressibility requirements, they are highly constrained and locking occurs. Analysis techniques that address volumetric locking are discussed in Techniques for reducing volumetric locking.

Plot the maximum in-plane principal stress in the model. Follow the procedure given below to create a filled contour plot on the actual deformed shape of the mount with the plot title suppressed.

To contour the maximum principal stress:

1. By default, Abaqus/CAE displays S, Mises as the primary field output variable. In the Field Output toolbar, select Max. Principal as the invariant.

   Abaqus/CAE automatically changes the current plot state to display a contour plot of the maximum in-plane principal stresses on the deformed model shape.

2. Open the Contour Plot Options dialog box.

3. Drag the uniform contour intervals slider to 8.

4. Click OK to view the contour plot and to close the dialog box.

   Create a display group showing only the elements in the rubber mount.

5. In the Results Tree, expand the Materials container underneath the output database file named Mount.odb.

6. Click mouse button 3 on RUBBER, and select Replace from the menu that appears to replace the current display with the selected elements.

7. The viewport display changes and displays only the rubber mount elements, as shown in Figure 5.

   Figure 5. Contours of maximum principal stress in the rubber mount.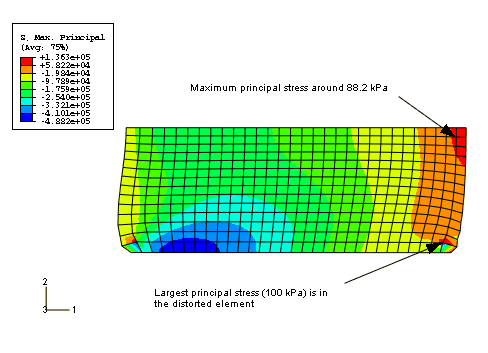
   
   

The maximum principal stress in the model, reported in the contour legend, is 136 kPa. Although the mesh in this model is fairly refined and, thus, the extrapolation error should be minimal, you may want to use the query tool to determine the more accurate integration point values of the maximum principal stress.

When you look at the integration point values, you will discover that the peak value of maximum principal stress occurs in one of the distorted elements in the bottom right-hand part of the model. This value is likely to be unreliable because of the levels of element distortion and volumetric locking. If this value is ignored, there is an area near the plane of symmetry where the maximum principal stress is around 88.2 kPa.

The easiest way to check the range of the principal strains in the model is to display the maximum and minimum values in the contour legend.

To check the principal nominal strain magnitude:

1. From the main menu bar, select ViewportViewport Annotation Options.

   The Viewport Annotation Options dialog box appears.

2. Click the Legend tab, and toggle on Show min/max values.

3. Click OK.

   The maximum and minimum values appear at the bottom of the contour legend in the viewport.

4. In the Field Output toolbar, select Primary as the variable type if it is not already selected.

   Abaqus/CAE automatically changes the current plot state to display a contour plot of the maximum in-plane principal stresses on the deformed model shape.

5. From the list of output variables, select NE.

6. From the list of invariants in the Field Output toolbar, select Max. Principal if it is not already selected.

   The contour plot changes to display values for maximum principal nominal strain. Note the value of the maximum principal nominal strain from the contour legend.

7. From the list of invariants, select Min. Principal.

   The contour plot changes to display values for minimum principal nominal strain. Note the value of the minimum principal nominal strain from the contour legend.

The maximum and minimum principal nominal strain values indicate that the maximum tensile nominal strain in the model is about 100% and the maximum compressive nominal strain is about 56%. Because the nominal strains in the model remained within the range where the Abaqus hyperelasticity model has a good fit to the material data, you can be fairly confident that the response predicted by the mount is reasonable from a material modeling viewpoint.