CZone analysis

Introduction

The use of composites in automotive, aircraft, marine, military, and other equipment requires composites to be designed for predictable behavior both under normal loads and under extreme conditions. For example, energy absorption and failure of composite automotive body panels as they are crushed help protect the vehicle’s occupants in an accident. A rectangular cross-section cone designed for energy absorption upon impact is shown in Figure 1. Most of the composite cone crushes during the experiment to stop the test sled. Figure 1 also shows a small portion of the cone remaining intact at the end of the experiment.

Figure 1. The plain cone test setup (left) and the plain cone sample at test completion (right) (courtesy of Engenuity, Ltd.).

The crushing behavior of composites is a complex finite element analysis problem that generally cannot be described by conventional failure mechanisms designed to simulate metal components. The material layers, reinforcements, and bonding between layers in a composite each have different failure characteristics. The load-carrying capacity of the composite is controlled by localized buckling, shearing, delamination, and eventual failure of the composite material in the area being crushed. While a material is crushed, it continues to transmit stress in a zone of damage called the crush front or crush zone, immediately adjacent to the point of impact between the composite and the object that is crushing it. Not all materials can be crushed. Physical testing is required to determine whether a material can be crushed and the characteristics of its behavior while being crushed.

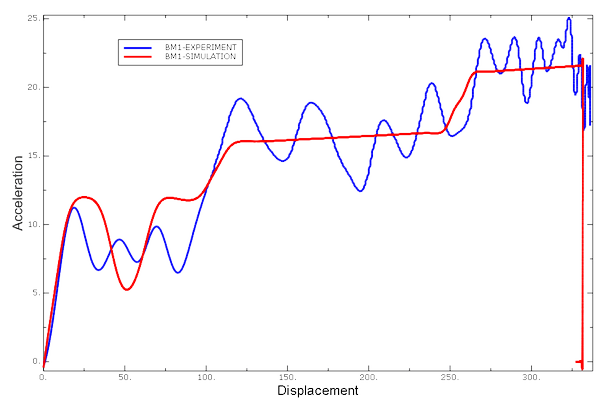
The CZone for Abaqus capability integrates material, element, and contact algorithms to simulate continuous crushing behavior. Figure 2 compares sled acceleration histories for the experiment associated with Figure 1. The experimental and simulation acceleration curves match well, with the simulation results smoother than the experimental data. Conventional material damage and element failure mechanisms for finite element analysis tend to produce noisy acceleration and stress solutions for crushing phenomena, due to sequences of element failure followed by a short interval of no contact until additional elements of the crushing body are impacted. Conventional approaches typically underestimate energy absorption associated with crushing, unlike the CZone approach.

Figure 2. History of the sled acceleration for CZone for Abaqus simulation and experiment.

CZone methodology

Figure 3 shows a simple example of a crushable shell interacting with a rigid body with the CZone capability. The example represents a situation in which a thin part modeled with shells with initial velocity, $v_{o}$ , is crushed against a fixed rigid body using the CZone capability. During active crushing, the magnitude of the contact pressure is governed by the crush stress of the underlying material. In this example the magnitude of the contact pressure (shown in blue in Figure 3) does not change while crushing is active.

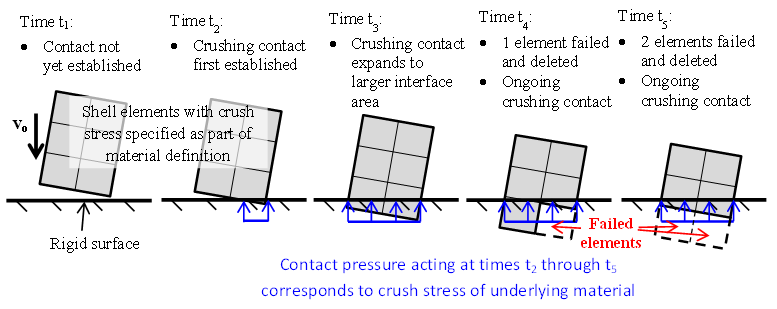
Figure 3. CZone continuous crushing sequence.

Significant penetrations can occur as a result of limiting the contact pressure to the crush stress of the underlying material. Shell elements involved in CZone crushing fail and are deleted once all nodes of a shell element penetrate the surface being impacted, such as in the configuration on the right side of Figure 3.

The crush stress can account for various material failure mechanisms, such as delamination, matrix cracking, fiber breakage, fiber pull-out, and fiber buckling, although the CZone capability does not attempt to distinguish between the various failure mechanisms. Even though the crush stress is specified as a material characteristic, the direct effect of the crush stress is limited to the contact pressure calculations; that is, constitutive (material) calculations for elements that are still active do not consider crush stress aspects of the material definition.

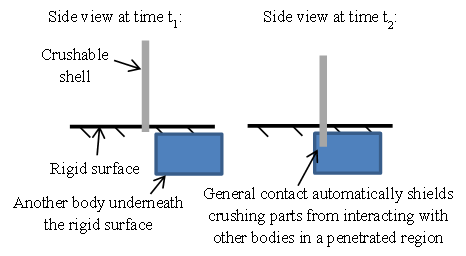
As discussed in the context of Figure 3, penetrations on the order of element dimensions are expected in the crushing region. The implementation of the CZone capability in general contact includes a shielding mechanism to avoid undesired secondary contacts for parts undergoing crushing. For example, this shielding mechanism avoids undesired interactions between the crushable shell and the body below the thin rigid body in Figure 4.

Figure 4. Example of automatic shielding from secondary contacts during CZone crushing.

Overview of model set-up aspects of CZone

Model specification aspects associated with CZone include:

Modeling potentially crushing parts with shell elements (see Shell elements);
Specifying crush stress characteristics in the material definition associated with potentially crushing parts (see CZone crush stress);
Including surfaces involved in crushing contact in the general contact definition (see About general contact in Abaqus/Explicit);
Optionally, specifying nondefault crush initiation characteristics as surface properties (see Assigning surface properties for general contact in Abaqus/Explicit);
Optionally, specifying other failure mechanisms (see Progressive Damage and Failure); and
Optionally, requesting CZone output.

CZone crush stress

The crush stress can be thought of as the stress of the crushing body at the crushing interface. The crush stress is specified as a material property but actually does not directly influence the constitutive calculations associated with element integration points; rather, the crush stress limits the contact pressure magnitude at an actively crushing interface.

The crush stress in the composite material can be a constant or can vary as a function of the angle, $θ,$ between the local x-direction of the crushable element and the contact normal direction projected to the plane of the element.

Input File Usage

Use the following option to define a constant crush stress:

CRUSH STRESS
crush stress

Use the following option to define the dependence of crush stress on the angle $θ :$

CRUSH STRESS
crush stress, material angle in degrees

For example:

CRUSH STRESS
90.0, 0.0
60.0, 45
90.0, 90
60.0, 135
90.0, 180

Crush stress as a function of a field variable

The crush stress in the composite material can vary as a function of a predefined field variable. This field variable can represent any physical or geometrical quantity that might affect the crush stress, such as curvature of the laminate.

Input File Usage

Use the following option to define the crush stress as a function of a field variable:

CRUSH STRESS, DEPENDENCIES

For example, the following definition can be used to define a crush stress that increases by 10% in curved regions of the model versus flat regions. The example assumes that curvature information is defined by the second field variable (FV2), which has been initialized with a value of one at the nodes in the curved regions of the model and a value of zero in the flat regions. Field variable dependency is evaluated only at the beginning of the analysis. Subsequent changes in the field variable will have no effect on the crush stress of the material.

CRUSH STRESS, DEPENDENCIES=5
90.0,   0.0, , , 0.0
60.0,  45.0, , , 0.0
90.0,  90.0, , , 0.0
60.0, 135.0, , , 0.0
90.0, 180.0, , , 0.0
99.0,   0.0, , , 1.0
66.0,  45.0, , , 1.0
99.0,  90.0, , , 1.0
66.0, 135.0, , , 1.0
99.0, 180.0, , , 1.0

Crush stress as a function of velocity

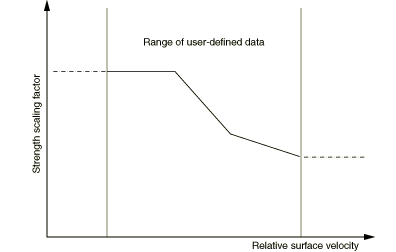
The crush stress in the composite material can depend on the deformation rate at the crush front. The crush stress velocity factor is used to scale the crush stress based upon velocity. The scaling factor is calculated from a user-supplied table of scaling factor versus relative surface velocity.

The final crush stress is the velocity dependence factor multiplied by the original crush stress. No extrapolation of the supplied data is performed for velocities that lie outside the maximum or minimum value supplied, as shown in Figure 5.

Figure 5. Crush stress is held constant outside of the supplied data range.

Input File Usage

Use the following option to specify the crush stress velocity factor:

CRUSH STRESS VELOCITY FACTOR

For example:

CRUSH STRESS VELOCITY FACTOR
1.5, 0.0
1.5, 1.0
1.25, 10.0
1.0, 100.

Contact limitations for CZone for Abaqus

The following limitations currently exist for CZone for Abaqus:

Crushable bodies can be modeled only with shell elements (see Shell elements).
Only node-to-surface contact is supported. Edge-to-edge contact is automatically deactivated for nodes involved in crushing; however, edge-to-edge contact may be active for nodes on crushable bodies that are not crushing.
Crushing calculations cannot involve analytical rigid surfaces.

Complex intersections and domain decomposition in CZone for Abaqus

Figure 6 shows a close-up view of a part with a T-junction geometry crushing against different sides of a folded shell in different regions. The folded shell experiences self-contact. This example shows that crushable bodies can have complex geometries, that crushing can occur with a double-sided target surface, and that noncrushing contact can occur nearby crushing contact.

Figure 6. Crushing of a T-junction part against a folded shell surface.

The implementation of CZone for Abaqus allows the crushing region to be split across domains for domain decomposition associated with distributed memory parallelization.

Material models to predict noncrushing failure mechanisms (generally available in Abaqus)

Composite layers can be modeled as an anisotropic linear elastic material or as a material with a viscoelastic response as described below.

Material anisotropy

Modeling each composite layer as an anisotropic linear elastic material is a valid assumption for composite materials that fail when a specific criterion is met, usually at small strain levels.

The parametric input capability provides a convenient method to define the material model parameters in an Abaqus input file; see Parametric Modeling for more information. Parametric input allows you to easily visualize and edit the material definition in the input file.

Input File Usage

The following example shows the usage of the parametric input capability:

*PARAMETER
E1 = 52500.
E2 = 52500.
nu12 =0.04
nu21 = E2 * nu12 / E1
G12 = 4700.
G13 = 4700.
G23 = 4700.
*ELASTIC, TYPE=LAMINA, MODULI=LONG TERM
<E1>,<E2>,<nu12>,<G12>,<G13>,<G23>

Material viscoelasticity

Many composite materials subject to dynamic crush loading exhibit rate-dependent stiffness. The material damping in CZone for Abaqus is represented as material viscoelasticity. The viscoelastic response is modeled using a Prony series fit to the experimental data. Typically, several different experimental tests could be used to determine the viscoelastic response. However, the stiff nature of composite materials makes it difficult to carry out the required experimental tests. Dynamic Mechanical Analysis (DMA)—a test usually associated with testing polymer viscoelasticity—can provide the necessary results within a limited frequency range. The DMA test provides values of storage and loss moduli versus frequency. These frequency-dependent data can be converted into the required nondimensional coefficients to define the viscoelastic material parameters; for more information on specifying the frequency-dependent test data, see Determination of viscoelastic material parameters.

Crush state evolution

Table 1 summarizes the possible crush state settings for slave nodes. The values in the first column of Table 1 are reflected in the output variable CRUSHSTATE. Nodes can have initial states of "not crushable" (0), "non-trigger" (1), or "trigger" (2). "Not crushable" nodes have no crush associated with adjacent elements and will never crush. "Non-trigger" nodes will be reassigned "trigger" status during the simulation if adjacent nodes begin crushing or adjacent elements experience material failure.

Upon coming into contact, a "trigger" node develops contact pressures consistent with the assigned contact pressure-overclosure relationship (see Contact pressure-overclosure relationships) and becomes an "actively crushing" node if either of the following conditions are met:

the contact pressure acting in the plane of the crushable material underlying the slave surface reaches the crush initiation stress, and the angle between contacting surfaces is greater than the crush initiation angle; or
an adjacent slave node is actively crushing, and the angle between contacting surfaces is greater than the crush continuation angle.

By default, the crush initiation stress is equal to the crush stress, but you can specify a scale factor to increase the crush initiation stress above the default value. Default thresholds of crush initiation and crush continuation are 30° and 25°, respectively. The angle between contacting surfaces is always in the range of 0° to 90°, so resetting either threshold angle to 0° results in all contacts meeting the respective angle threshold.

Table 1. Crush state settings for slave nodes.
Value of Output Variable CRUSHSTATE	Description	Behavior
0	Not crushable node	This node will never crush; no crush stress is associated with this node.
1	Non-trigger node	This node is not a trigger node and had no prior crushing.
2	Trigger node	This node is a trigger node and had no prior crushing.
3	Previously crushing node	This node was previously crushing.
4	N/A (this setting is not used)
5	Actively crushing node	This node is actively crushing.
6	Failed node	This node has "failed" as a result of crushing or material failure.

Contact forces for nodes with "actively crushing" status are equal to the crush stress times the crush area. A slave node continues crushing until:

It comes out of contact or the angle between contacting surfaces falls below the crush continuation angle. In this case the nodal state is reset to "previously crushing."
All adjacent elements are deleted due to crushing or other types of material failure. In this case the nodal state is "failed."

A node with a "previously crushing" status resumes crushing if the angle between contacting surfaces is greater than the crush continuation angle and either of the following conditions are met:

the contact pressure acting in the plane of the crushable material underlying the slave surface reaches the crush stress; or
an adjacent slave node is actively crushing.

Input File Usage

Use the following option to initialize a node to "trigger" status (default) and to specify a crush initiation scale factor, crush initiation angle, and crush continuation angle:

SURFACE PROPERTY ASSIGNMENT, PROPERTY=CRUSH TRIGGER
surface name, TRIGGER, scale factor, crush initiation angle, crush continuation angle

Use the following option to initialize a node to "non-trigger" status, and (in case the node later becomes a trigger node) to specify a crush initiation scale factor, crush initiation angle, and crush continuation angle:

SURFACE PROPERTY ASSIGNMENT, PROPERTY=CRUSH TRIGGER
surface name, NO TRIGGER, scale factor, crush initiation angle, crush continuation angle

Use the following option to initialize a node to "not crushable" (no crush) status:

SURFACE PROPERTY ASSIGNMENT, PROPERTY=CRUSH TRIGGER
surface name, NO CRUSH

Influence of noncrushing failure mechanisms on crush initialization

When a crushable body first comes into contact during the analysis, the contacting nodes may not crush initially. During this period, the internal stress within the element may become large enough to initiate material failure.

Testing crush behavior

Until the micromechanics of crushing failure mechanisms are more fully understood, it is necessary to test the crush properties of candidate materials. There are several methods to test crush strength; some of these methods are still evolving. Once the crush strength is determined, the crush stress for the composite can be calculated.

This section discusses three methods used to test the crushing properties of composite materials. To obtain the best simulation results, the tests used to determine the crushing properties should represent the design structure as closely as possible.

Ultimately, you must decide which method of crush strength measurement to use in determining the crush stress values to input for the CZone for Abaqus analysis. Regardless of the method selected, the coupon design should have a thickness and layup consistent with the structure being developed.

Component testing

In the component testing method a component is manufactured from the candidate material. The component geometry should support crushing, such as a straight box or similar section with a side length to wall thickness ratio that prevents local buckling. This is the most accurate testing method; however, it is also relatively costly. This approach involves the following steps:

Crush the component using an impact sled.
Measure the acceleration of the sled.
Calculate the crush force from the acceleration.
Calculate the crush stress by dividing the crush force by the cross-sectional area of the component.

The high cost of this test method has led to the development of lower cost coupon test methods described in the following sections.

Flat coupon testing

Several organizations are developing the flat coupon testing method. Test coupons are typically cut from a flat sheet using a water jet to minimize damage at the cut edges. One end of the coupon is weakened by incorporating a saw-tooth shape or chamfer to initiate crushing. The flat coupon is placed in a fixture that prevents buckling. A drop-tower or servo-hydraulic test apparatus is used to push the coupon through the fixture onto a crushing or target plate. The ongoing crush force is divided by the cross-sectional area of the flat coupon to determine the crush strength.

In the flat coupon testing method, the coupon typically has a region near the crushing end that is free from support or constraint. This region is the unsupported length. Figure 7 shows a coupon crushing fixture installed in a servo-hydraulic dynamic testing apparatus.

Figure 7. Flat coupon test apparatus (courtesy of Engenuity, Ltd.).

Figure 8 shows how the material crushes at the lower end of the fixture as it is forced down through the fixture's low-friction guides. The fixture has adjustments for different coupon thicknesses and for varying the unsupported length.

Figure 8. Crushing a flat coupon (courtesy of Engenuity, Ltd.).

Shaped coupon testing

Several organizations are developing the shaped coupon testing method. The test coupons are shaped with corrugations to give them stability when they are crushed on a flat surface. Like the flat coupons, one end of the shaped coupon is weakened with a saw-tooth shape, as shown in Figure 9, or a chamfer to initiate crushing.

Figure 9. A typical shaped coupon used for crush testing (courtesy of Engenuity, Ltd.).

Figure 10 shows the shaped coupon after testing.

Figure 10. The crushed shaped coupon (courtesy of Engenuity, Ltd.).

The shaped coupons are more expensive than the flat coupons but still significantly less expensive than producing custom test components.

Comparison of flat and shaped coupon tests

Many composites exhibit ongoing delamination in the crush zone as part of the crushing process. Shaped coupons tend to suppress delamination, often leading to a higher value for the crush stress than the flat coupons, which allow delamination more readily. The ratio of the measured crush stresses from the shaped and flat coupon methods varies with the material.

Most composite structures consist of both flat and curved regions. To evaluate a realistic crush performance for these structures, it is recommended to test samples using both coupon methods. You can then assign the flat coupon crush stress values to flat regions and the shaped (suppressed delamination) crush stress values to curved regions. This approach is illustrated in Figure 11.

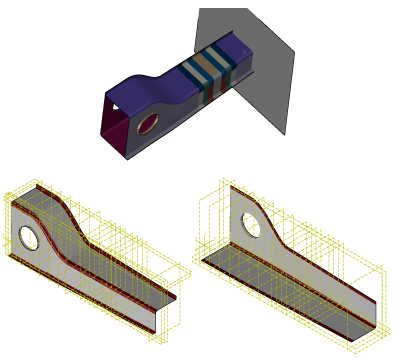
Figure 11. Identifying regions of higher crush resistance based on curvature.

The top image shows a CZone for Abaqus analysis of a cone made from two components joined at the flanges. The bottom images show the regions of crush stress assignment in the two pieces that make the cone. The corner radius areas, including the flange areas where the two pieces are joined, help to suppress delamination. They are assigned a delamination suppressed crush stress of 122 MPa. The flat areas are assigned a flat coupon crush stress of 50 MPa. The physical test of the component yielded an average crush stress of 77 MPa.

Some materials have a high resistance to delamination, such that the flat and shaped coupon test methods converge toward a common crush stress value. Further research is being conducted into methods of suppressing delamination in the flat coupon test method to determine the elevated crush strength values while using the low cost flat coupons.

Output

Viewing the results of a CZone for Abaqus analysis is comparable to viewing the results of other Abaqus analyses. To understand the results of a crushing analysis, you should review the output results associated with the CZone crushing state, the material damage, and the energy quantities in the Visualization module of Abaqus/CAE. For general information on viewing results, see Viewing results.

CZone crushing state and material damage variable output

CZone for Abaqus uses the contact output variable CRUSHSTATE to report information about the current crushing state of the nodes on the slave surface (see Table 1).

In addition, you should request output of the relevant damage variables in accordance with the composite damage model used in the simulation. For example, for the Tsai-Wu criterion you need output of solution-dependent state variables, and for the Hashin damage model you need output of the damage variables documented in Output. You can use these results to determine the regions that failed due to crushing and those that failed as a result of composite damage and failure.

Highlighting failed regions

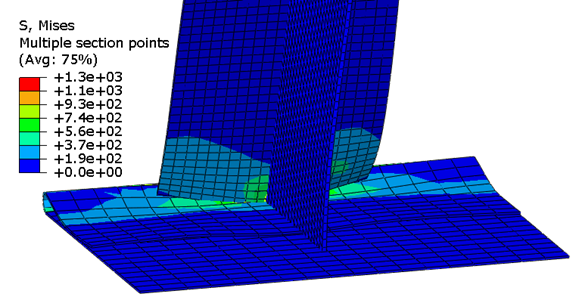
Plot the contours of CRUSHSTATE on the undeformed shape to highlight the regions that have failed or are starting to fail as a result of crushing. The regions where CRUSHSTATE is six (colored red in Figure 12) have failed as a result of crushing. Regions where CRUSHSTATE is five (colored yellow) are currently crushing.

Figure 12. Plotting output variable CRUSHSTATE on the undeformed shape.

Removing failed elements from the view

You can use ResultField OutputStatus Variable to remove the failed elements from the view. Select CZASTATE as the output variable, and remove elements with a value greater than 3; select Apply to undeformed state to remove the elements from the undeformed model view. The result is shown in Figure 13.

Figure 13. Fragments that broke away from the model as the surrounding elements failed.

Removing elements that failed due to material damage

If you use the Tsai-Wu damage initiation model, you can remove the elements that have failed as a result of material damage. Select SDV3 to be the status variable, and remove elements whose SDV3 value is greater than 0.99, as shown in Figure 14.

Figure 14. Removing elements that have failed as a result of material damage.

If you are using the Hashin damage model, you can request the damage output variables associated with different damage mechanisms to evaluate the dominant damage mode (see Output).

Example crushing simulations

This section contains two benchmark simulations that you can use as guides for creating new analyses. An input file for each benchmark problem can be extracted as described in Fetching sample input files.

Plain cone

In this benchmark a rectangular cross-section cone is attached to a rigid wall, as shown in Figure 15, and impacted with a moving sled with a mass of 324 kg and an initial velocity of 10m/s. The input file for this example is cza_bm1-cone-ahv_gc.inp.

The layup of the composite cone includes three different thickness regions. It is thinnest at the front (left side of the plain cone test setup) and gets thicker toward the rear (right side of the plain cone test setup), as shown in Figure 15. The thickness at the front of the cone is such that local buckling occurs and fragments of material break away due to bending stresses. As crushing progresses, the increased wall thickness allows progressive crushing of the cone without buckling and bending failure. Figure 15 shows the final crushed state of the cone.

Figure 15. The plain cone test setup (left) and the plain cone sample at test completion (right) (courtesy of Engenuity, Ltd.).

Figure 16 shows some material fragments that broke away from the front of the cone.

Figure 16. Fragments taken from the experimental test (courtesy of Engenuity, Ltd.).

The tapered colored markings on the fragments indicate that they came from the front of the cone on the long sides. The fragments that were predicted to break out from the thin part of the cone in the simulation match well with the test fragments, as shown in Figure 17.

Figure 17. Fragments that broke away during the simulation.

The predicted sled acceleration curve also matches well with the test data, as shown in Figure 18.

Figure 18. History of the sled acceleration for the simulation and experiment.

Complex cone

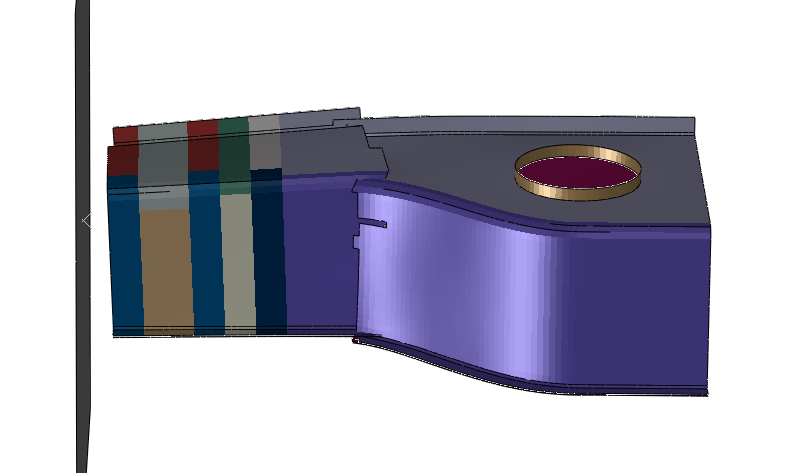
In this benchmark a complex cone is attached to a moving sled, as shown in Figure 19, and impacted against a wall. The input file for this example is cza_bm3-b-cone-ahv_gc.inp. The sled has a mass of 1150 kg and an initial velocity of 9.1 m/s.

Figure 19. Experimental setup for the complex cone (courtesy of Engenuity, Ltd.).

The component geometry is intended to represent some of the typical features and general size of a typical automotive front longitudinal member. The layup of this component was designed to behave in a way that shows an initial period of crushing, followed by catastrophic failure of the backup structure. At the front of the component the layup is relatively thin, and the backup structure is strong enough to support the crushing forces. As crushing progresses, the thickness of the layup progressively increases. At a certain point the back of the cone can no longer support the increased crushing forces from the thicker material, and failure occurs at the curved transition area—this quickly propagates around the section and the cone breaks in two. Figure 20 and Figure 21 show experimental and analysis results, respectively, at the point of failure.

Figure 20. Experimental results for the complex cone (courtesy of Engenuity, Ltd.).

Figure 21. Simulated failure of the complex cone.

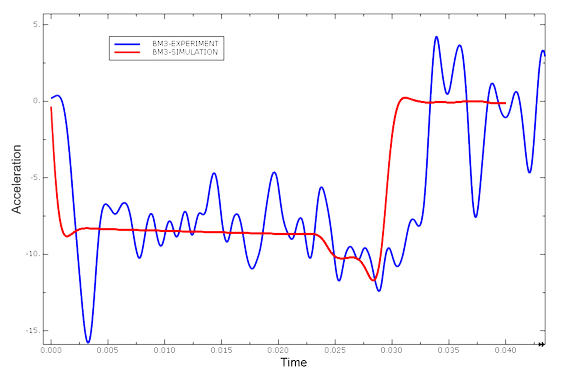
Acceleration histories of the experimental and analysis results correlate well, as shown in Figure 22. The acceleration of the analysis approaches a constant value near zero after the crushing event, as shown by the red curve. The acceleration of the experimental results exhibit some experimental noise after passing through zero, as shown by the blue curve.

Figure 22. Time history of the sled acceleration for the complex cone.

Verification tests

This section contains a series of verification tests for CZone for Abaqus. These simple problems are intended to demonstrate some of the capabilities of the CZone methodology used with an Abaqus/Explicit analysis and to allow you to confirm the results. An input file for each verification problem can be extracted as described in Fetching sample input files.

Single strip

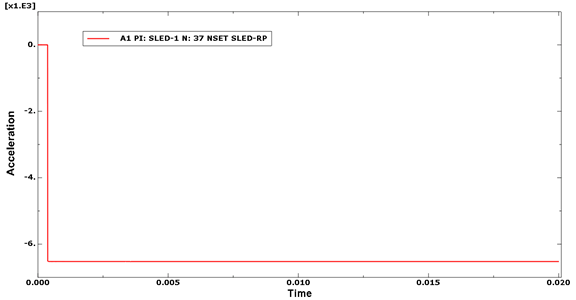
This first, simple example tests the failure of elements and the correct calculation of the crushing forces through the CZone for Abaqus interaction. A sled, modeled as a discrete rigid body, impacts a simple composite strip. The composite strip has an encastre boundary condition at one end and is constrained to remain planar. The acceleration versus time history should be constant once the crushing mode is established. The crushing stress for the material is independent of the direction in which it is being crushed.

The results are obtained by running cza_v1_gc.inp. The time history of the sled acceleration (history variable Spatial acceleration: A1 PI: SLED-1 Node 37 in NSET SLED-RP) should be plotted to confirm the constant loading, as shown in Figure 23.

Figure 23. The time history of acceleration for the single strip.

Angled strip

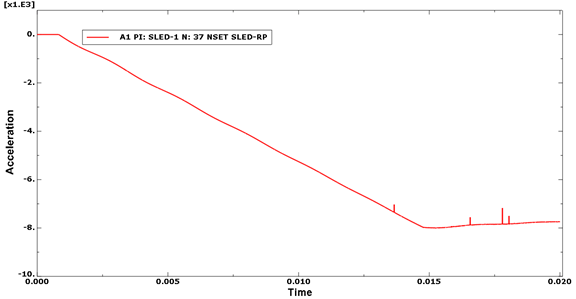
In this test the plate is angled relative to the strip of composite material. The crushing force should gradually increase as the sled makes contact with the strip before the crushing force becomes approximately constant. The crushing stress for the material is independent of the direction in which it is being crushed.

The results are obtained by running cza_v2_gc.inp. The time history of the sled acceleration (history variable Spatial acceleration: A1 PI: SLED-1 Node 37 in NSET SLED-RP) should be plotted to confirm the loading, as shown in Figure 24.

Figure 24. The time history of acceleration for the angled strip.

Bounce (oblique impact)

CZone for Abaqus contact definitions are described in CZone methodology. This example tests an oblique (non-crushing) impact. The input file for this example is cza_v3_gc.inp. A composite strip is moving toward an oblique rigid plate, which is constrained in all degrees of freedom. The composite structure should hit and bounce clear from the plate. The filtered time history of the force on the rigid reference node of the plate is shown in Figure 25.

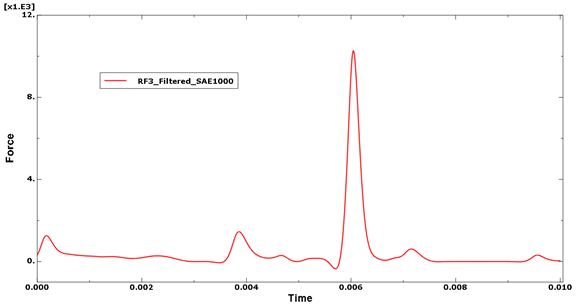
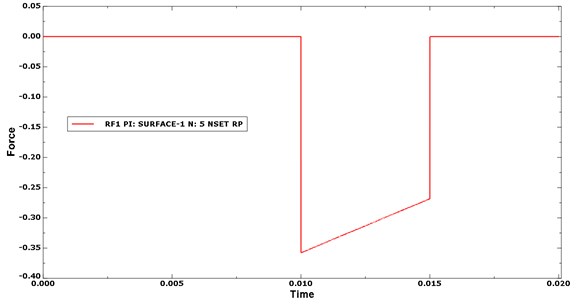
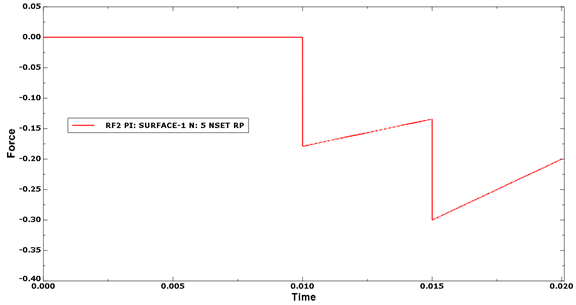
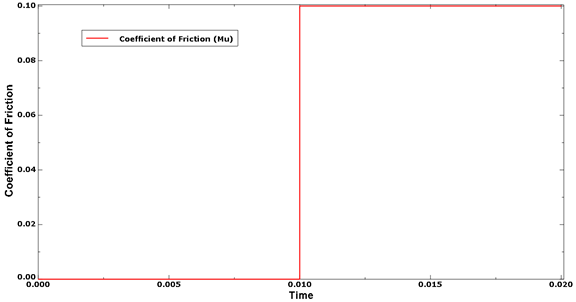
Figure 25. The time history of the force on the rigid reference node.

Friction

A very simple test is performed to check the friction calculations. The input file for this example is cza_v4_gc.inp. Two parts are defined, each containing a single element, but one part larger than the other. The larger part is a rigid surface, encastre at the rigid reference node, and the other is a very simple composite layup with two plies. The two parts are pressed together by a distributed load acting on the composite. Relative motion between the surfaces is induced by boundary conditions acting at the corner points of the composite element. The effective coefficient of friction can be calculated by monitoring the reaction force in the 1- and 2-directions and dividing it by the reaction force in the 3-direction. Figure 26 and Figure 27 show the friction forces in the 1- and 2-directions, respectively. The friction coefficient is shown in Figure 28.

Figure 26. The time history of friction force in the 1-direction.

Figure 27. The time history of friction force in the 2-direction.

Figure 28. Time history of the friction coefficient.

Five finger

In this test a single composite specimen, with five fingers and a central palm, is completely constrained. The composite has a simple layup composed of 10 layers of orthotropic material. The crush resistance is a function of angle for this material defined for the crush stress. The input file for this example is cza_v5_gc.inp.

Five individual sleds are defined, each paired with a finger on the composite component, as shown in Figure 29.

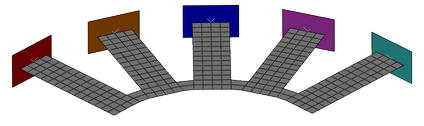
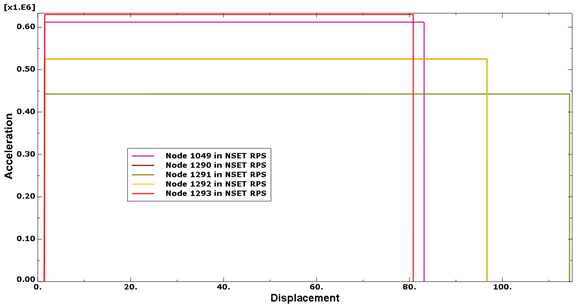
Figure 29. The initial configuration of the five finger model.

The sleds travel toward and along the length of the fingers with an initial velocity. The progress of the sleds is resisted by the force required to crush the composite fingers. The angular dependence of the crush resistance means that each sled travels a different distance along the fingers. The displacement versus acceleration for each sled is shown in Figure 30.

Note:

Two of the curves—the ones for nodes 1290 and 1292—are identical, so there appear to be only four curves in the graph. This is the result of the angular properties of the second and fourth fingers having identical crushing properties in the test direction.

Figure 30. The displacement versus acceleration for each of the five sleds.

Velocity dependence

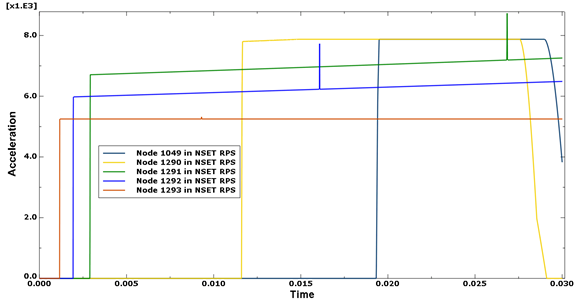
This test uses the same composite geometry and layup of the Five finger test. In this case the crush resistance is a function of crush velocity instead of angle. The crush stress velocity factor defines a scaling factor that is applied to the crush resistance based on velocity. The input file for this example is cza_v6_gc.inp.

Five individual sleds are defined, each paired with a finger on the composite component, as shown in Figure 29. Each sled travels with a different initial velocity defined along the length of the finger. The progress of the sleds is resisted by the force required to crush the composite fingers. The velocity-dependent crush properties and the different initial velocities generate a different crushing resistance and, therefore, a different acceleration, for each sled (see Figure 31).

Figure 31. The time history of acceleration for the five sleds with different initial velocities.

Oblique box (general contact, fixed wall, moving cone)

The geometry and layup of the plain cone benchmark is reused in this verification problem. For information about the model, see Plain cone. The cone is rotated relative to the sled, and the sled is constrained to remain stationary. An initial velocity of 10 m/s is applied to the cone and to the 500 kg mass attached to the back of the composite structure. The input file for this example is cza_v7_gc.inp.

A combination of crushing and brittle failure is predicted by the model. As the front face of the cone makes contact with the rigid surface, it exhibits brittle failure, peeling along the edges that join it to the side walls. This exposes new edges to a crushing interaction with the rigid surface. The mixture of brittle failure and crushing produces a noisy reaction force at the rigid reference node.

Leading edge (airfoil/F1 wing)

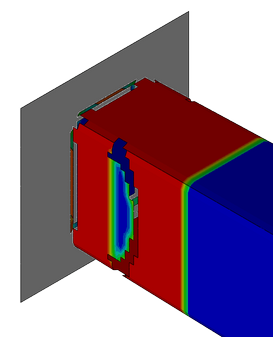
Here, a simplified airfoil representing the nose cone of a Formula One car makes contact with a rigid pole. The input file for this example is cza_v8_gc.inp. The car is traveling at approximately 140 km/h. The initial impact causes brittle failure on the leading edge as the composite makes contact with the cone. The model setup is shown in Figure 32 and Figure 33.

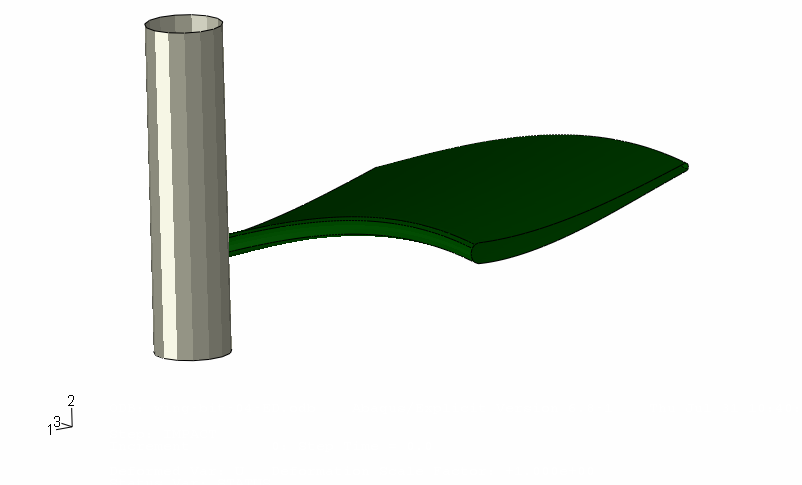
Figure 32. Airfoil contact, side view.

Figure 33. Airfoil contact, front view.

After initial impact, the failure mode becomes crushing as the impact continues and new composite material is exposed. Eventually the forces become too great, and failure is observed where the airfoil joins the nose (the boundary condition on the edge of the airfoil away from the pole). As this failure occurs, the composite structure rotates and the crushing ceases. This verification problem tests the implementation of the Tsai-Wu failure criteria and the transition from bouncing (hard contact) to crushing.

The difference in the failure modes is shown in Figure 34 and Figure 35. All failed elements from both crushing and brittle failure have been removed from Figure 34. Only elements that failed as a result of crushing have been removed from Figure 35. The removal of failed elements in Abaqus/CAE is discussed in Output.

Figure 34. Airfoil with all failed elements removed.

Figure 35. Airfoil with only crushed elements removed.

Composite failure, part one

A tapered composite sample is crushed against a stationary rigid surface, as shown in Figure 36. The input file for this example is cza_v9_gc.inp.

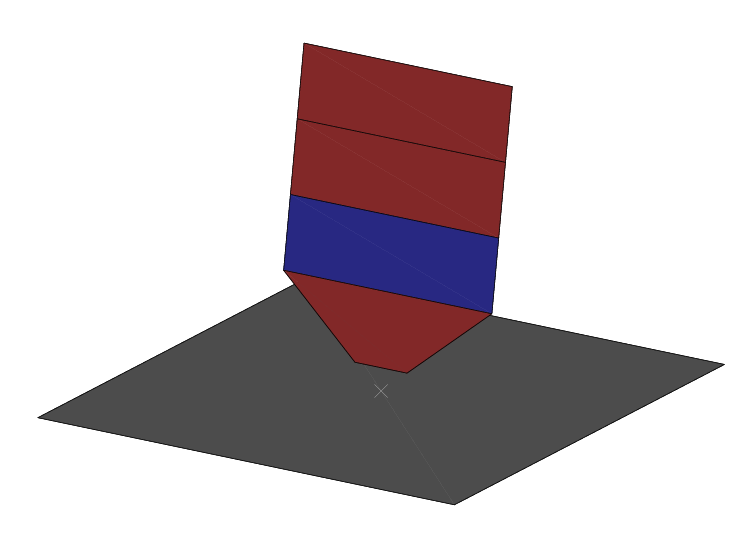
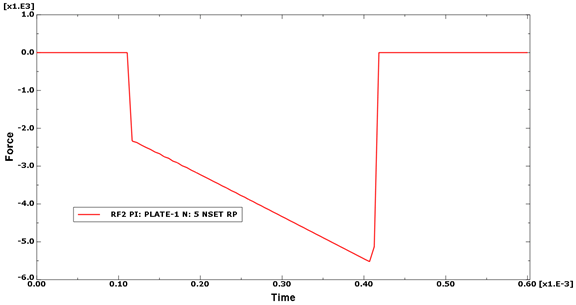
Figure 36. The composite failure model setup.

The crush force increases as the first tapered element crushes against the rigid surface. The increasing load causes the element behind the tapered element to fail as a result of brittle failure. The first element is free to bounce from the surface as the rest of the structure continues toward it. The reaction force at the rigid reference node is shown in Figure 37.

Figure 37. The reaction force at the rigid reference node.

Composite failure, part two

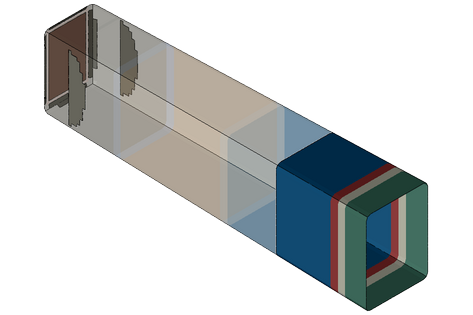
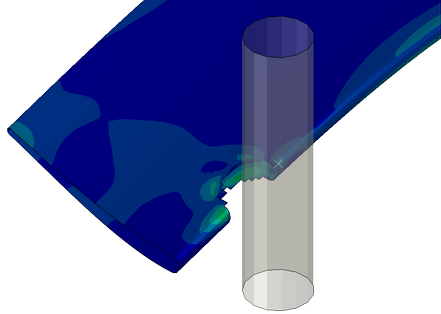
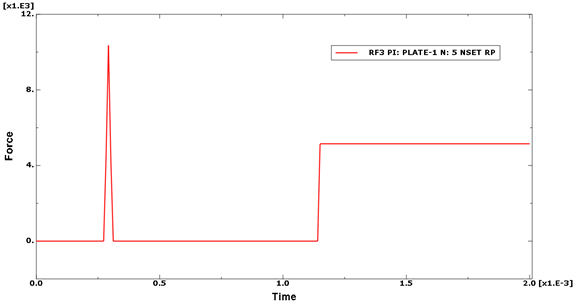
A coarse representation of a cylindrical component is used to test the damage and failure of elements close to the crush zone interaction. The input file for this example is cza_v10_gc.inp. The component, shown in Figure 38, is pushed against a flat, rigid, encastre surface.

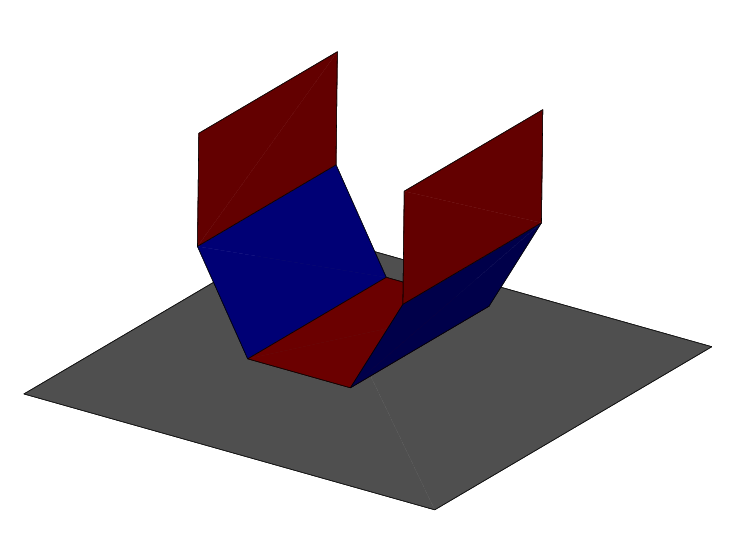
Figure 38. The composite failure model setup.

The first element bounces against the rigid surface and transfers the load through the neighboring elements to the rest of the structure. Eventually the two neighboring elements fail as a result of damage mechanisms. This releases the central element, which bounces from the surface. The component continues to move toward the rigid surface, and eventually the side walls begin to crush. The time history of the reaction forces is shown in Figure 39.

Figure 39. Reaction forces during the composite failure.

Input file template

The following template includes the basic Abaqus options and all of the available CZone for Abaqus options required to create a crushing analysis. There are two blocks in the template, each starting with a material definition. The first block is for use with Tsai-Wu damage initiation. The second block is for use with Hashin damage initiation. The rest of the template continues with all material references made to the Tsai-Wu model. The template uses the parts and instances input file format used in Abaqus/CAE; however, CZone for Abaqus does not require that you use this format.

HEADING
…

PART, NAME=Part-1
Node, element, section, set, and surface definitions
END PART
ASSEMBLY, NAME=Assembly-1
INSTANCE, NAME=i1, PART=Part-1
<positioning data>
Additional set and surface definitions (optional)
END INSTANCE
Assembly level set and surface definitions
…
END ASSEMBLY

**
**Material with Tsai-Wu damage
**
MATERIAL, NAME=material1
PARAMETER
Independent parameter definitions for plane stress orthotropic elasticity
ELASTIC, TYPE=LAMINA
Data lines to define the material constants
Data lines to define the material constants with damage evolution
DEPVAR, DELETE=1
Data lines to define the 3 dependent variables (status, Tsai-Wu, and stiffness degradation)
USER DEFINED FIELD, CZONE, PROPERTIES=16
Data lines to define Tsai-Wu failure stresses and the original material stiffness and absorbed energy
CRUSH STRESS
Data lines to define the crush stress as a function of orientation
CRUSH STRESS VELOCITY FACTOR
Data line to define the stress scaling factor as a function of relative velocity (optional)
**
**End Tsai-Wu material definition
**

**
**Material with Hashin damage
**

MATERIAL, NAME=material2
PARAMETER
Independent parameter definitions for plane stress orthotropic elasticity
ELASTIC, TYPE=LAMINA
Data lines to define the material constants
DAMAGE INITIATION, CRITERION=HASHIN
Data lines to define the Hashin failure criterion
DAMAGE EVOLUTION
Data lines to define the evolution of damage leading to eventual failure
CRUSH STRESS
Data lines to define the crush stress as a function of orientation
CRUSH STRESS VELOCITY FACTOR
Data line to define the stress scaling factor as a function of relative velocity (optional)
**
**End Hashin material definition
**


SURFACE INTERACTION, NAME=Int-1
FRICTION
Specify the friction coefficient

INITIAL CONDITIONS, TYPE=VELOCITY
Nodeset1, dof, initial_velocity

**
STEP, NAME=Step-1
DYNAMIC, Explicit
, time
**
**Optional boundary condition for use with CRUSH STRESS VELOCITY FACTOR
**
BOUNDARY, TYPE=VELOCITY
Data line to define stress scaling factor and relative velocity
CONTACT
CONTACT INCLUSIONS, ALL EXTERIOR
CONTACT PROPERTY ASSIGNMENT
 , , Int-1

**
**Output requests
**
RESTART, WRITE, NUMBER INTERVAL=integer, TIME MARKS=NO
OUTPUT, FIELD, VARIABLE=PRESELECT
...
Specify desired element, contact, and history output requests
END STEP