Overview of Internal Force

Parameter Name	Formula
INTERNAL_FORCE_ABS	$F = \sum_{} \| K_{e} u_{i} \|$
INTERNAL_FORCE_X, INTERNAL_FORCE_Y, INTERNAL_FORCE_Z	$F = \sum_{} K_{e} u_{i}$
INTERNAL_FORCE_X_ABS, INTERNAL_FORCE_Y_ABS, INTERNAL_FORCE_Z_ABS	$F = \sum_{} \| K_{e} u_{i} \|$
INTERNAL_MOMENT_ABS	$F = \sum_{} \| K_{e} u_{i} \|$
INTERNAL_MOMENT_X, INTERNAL_MOMENT_Y, INTERNAL_MOMENT_Z	$F = \sum_{} K_{e} u_{i}$
INTERNAL_MOMENT_X_ABS, INTERNAL_MOMENT_Y_ABS, INTERNAL_MOMENT_Z_ABS	$F = \sum_{} \| K_{e} u_{i} \|$

For the elements e attached to the nodes i.

Analysis Types: Static Linear or Non-Linear Analysis

K u = F

where K may be linear or non-linear.

For internal forces the following table shows the allowed combinations between strategy and the items OBJ_FUNC and CONSTRAINT with C for controller and S for sensitivity based optimization.

	TOPO	SHAPE	BEAD	SIZING
OBJ_FUNC	S	S	S	S
CONSTRAINT	S	S	S	S

The internal forces and the internal moments can be defined as a DRESP (design response) in the sensitivity-based optimization approaches.

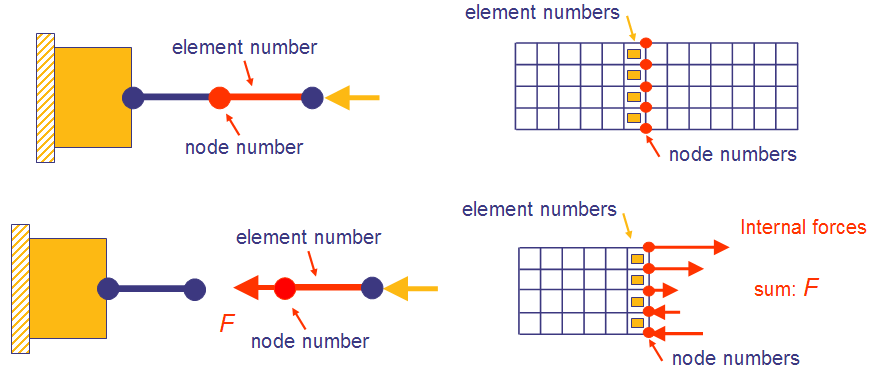
The internal forces as DRESPs are supported for Abaqus, MSC Nastran®. The following figure shows the definition of internal forces through nodes and elements. On the left the internal axial forces of a bar or beam is defined by using only one node and one element. On the right side the internal axial forces of a continuum element are defined by summing up the forces in axial direction using a node and an element group.

As previously shown the internal forces are defined by nodes and elements. Meaning that the design response is defined in the following way:

DRESP
 ID_NAME = .....
 DEF_TYPE = SYSTEM
 TYPE = .....
 CS_DEF = .....
 GROUP_OPER = MAX  or  SUM
 ND_GROUP = .....or use the NODE-definition
 NODE = .....or use the ND_GROUP-definition
 EL_GROUP = .....or use the ELEM-definition
 ELEM = .....or use the ELEM_GROUP-definition
 LC_SET = .....
END_

Important:

The reaction force, reaction moment, internal force and/or internal moment in a given DOF of a node applied in the optimization formulation has to have stiffness in the DOF direction similar to the DOF direction of the reaction force or internal force used in the optimization formulation. Meaning that at least one of the elements surrounding the node has to have stiffness in the DOF direction similar to the reaction force or internal force direction applied in the optimization formulation. Hence, this criterion is also physical meaningful since a structure having no stiffness in a given direction will always have zero reaction force in this direction.
Internal forces are only supported for elements having node numbers. If the element is not defined by nodes (e.g. some weld element) then the internal forces of this element cannot be applied in the optimization.
Both node(s) and element(s) always have to be defined for internal forces.
See also the tables of supported element types for a list of elements which can be used for internal forces.
A reference coordinate system (CS_REF) cannot be used for the internal force responses defined using INTERNAL_FORCE_ABS and INTERNAL_MOMENT_ABS.
Internal forces are supported for Abaqus and MSC Nastran®.