Group Operations for Internal Forces | ||
| ||
The picture below shows a structure where the internal forces in the y-direc tion of the two nodes 65 and 66 for elements 33, 34, 37 and 38 should be applied in a set of constraints using GROUP_OPER=MAX or GROUP_OPER=SUM.
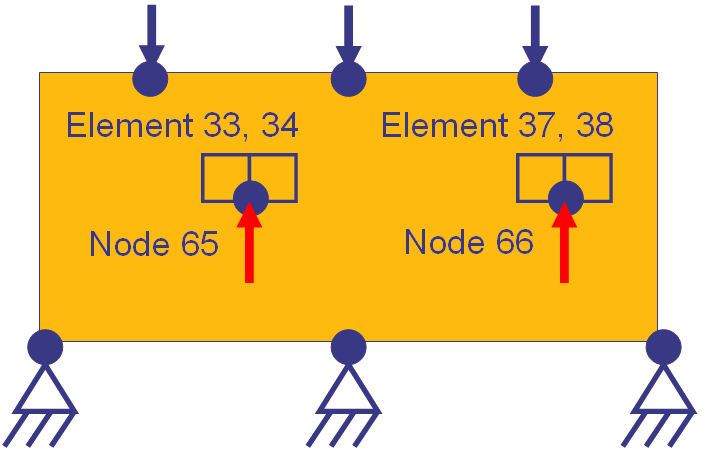 |
For the use in CONSTRAINTs is, initially, a node group defined containing the nodes 65 and 66 (see figure above) yielding
GROUP_DEF ID_NAME = FORCE_NODES TYPE = NODE FORMAT = LIST LIST_BEGIN 65, 66 END_
and a element group is defined containing the elements 33, 34, 37 and 38 (see figure above) yielding
GROUP_DEF ID_NAME = FORCE_ELEM TYPE = ELEM FORMAT = LIST LIST_BEGIN 33, 34, 37, 38 END_
GROUP_OPER = MAX
Based upon the node group and the element group a design response for the internal force in y-directions are defined in a DRESP using GROUP_OPER=MAX yielding
DRESP ID_NAME = DRESP_FORCE_MAX DEF_TYPE = SYSTEM TYPE = INTERNAL_FORCE_Y LC_SET = STATIC,1, ND_GROUP = FORCE_NODES EL_GROUP = FORCE_ELEM GROUP_OPER = MAX END_
Internally, SIMULIA Tosca Structure generates two DRESPs. One DRESP for the internal force of node 65 for element 33 and 34, and one DRESP for the internal force of node 66 for element 37 and 38.
If one then applies the DRESP in a constraint yielding:
CONSTRAINT ID_NAME = CONSTRAINT_MAX DRESP = DRESP_FORCE_MAX MAGNITUDE = ABS LE_VALUE = <value> END_
SIMULIA Tosca Structure then generates two internal force constraints like the following:
![]()
GROUP_OPER = SUM
Based upon the node group a design response for the internal force in y-directions are defined in a DRESP using GROUP_OPER=SUM yielding
DRESP ID_NAME = DRESP_FORCE_SUM DEF_TYPE = SYSTEM TYPE = INTERNAL_FORCE_Y LC_SET = STATIC,1, ND_GROUP = FORCE_NODES EL_GROUP = FORCE_ELEM GROUP_OPER = SUM END_
Internally, SIMULIA Tosca Structure generates one DRESP consisting of the sum of the internal forces of the nodes 65 and 66 for the elements 33, 34, 37 and 38.
If one then applies the DRESP in a constraint yielding:
CONSTRAINT ID_NAME = CONSTRAINT_MAX DRESP = DRESP_FORCE_MAX MAGNITUDE = ABS LE_VALUE = <value> END_
SIMULIA Tosca Structure then generates a single internal force constraint like the following:
![]()
Alternative Definition of Constraints Function
Alternatively, one could also define two DRESPs for each node like the following:
GROUP_DEF ID_NAME = FORCE_ELEM_1 TYPE = ELEM FORMAT = LIST LIST_BEGIN 33, 34 END_ DRESP ID_NAME = DRESP_FORCE_1 DEF_TYPE = SYSTEM TYPE = INTERNAL_FORCE_Y NODE = 65 EL_GROUP = FORCE_ELEM_1 LC_SET = STATIC,1 GROUP_OPER = MAX or SUM END_ GROUP_DEF ID_NAME = FORCE_ELEM_2 TYPE = ELEM FORMAT = LIST LIST_BEGIN 37, 38 END_ DRESP ID_NAME = DRESP_FORCE_2 DEF_TYPE = SYSTEM TYPE = INTERNAL_FORCE_Y NODE = 66 EL_GROUP = FORCE_ELEM_2 LC_SET = STATIC,1 GROUP_OPER = MAX or SUM END_
And then add the two design response in two constraints:
CONSTRAINT ID_NAME = CONSTRAINT_1 DRESP = DRESP_FORCE_1 MAGNITUDE = ABS LE_VALUE = <value> END_ CONSTRAINT ID_NAME = CONSTRAINT_2 DRESP = DRESP_FORCE_2 MAGNITUDE = ABS LE_VALUE = <value> END_
SIMULIA Tosca Structure then generates two internal force constraints like the following:
Consequently, it can be concluded that there is fundamental difference in the constraints if a node group (ND_GROUP) consisting of more than one node is applied and the choice of GROUP_OPER.