Surface-based acoustic-structural medium interaction

Abaqus provides two alternatives for modeling interaction between acoustic and structural media: surface-based interaction or acoustic interface (ASIn) elements. Both are available in Abaqus/Standard, but only the surface-based capability is available in Abaqus/Explicit. If the special-purpose interface elements (ASIn) are used, interacting structural and acoustic nodes must be shared by the two meshes. The surface-based capability can be used for structural and acoustic meshes that have different node numbering and whose surface meshes may not be spatially coincident. The ease of use and low computational cost of the surface-based procedure make it preferable to the element-based approach.

The following topics are discussed:

The equations on the contact interface between the structure and the acoustic medium
Solid/structural master, fluid slave
Fluid master, solid/structural slave

The equations on the contact interface between the structure and the acoustic medium

In the surface-based method the tractions and volumetric acceleration fluxes are computed between structural and acoustic media. In place of consistent distributed tractions or fluxes on both media, one side (identified as the “slave”) receives point tractions/fluxes based on interpolation with the shape functions from the other (“master”) side. Either the acoustic fluid or the structural solid can be the slave or master, and no Lagrange multipliers are introduced in the formulation. The basis for deciding which to make slave or master is discussed in Acoustic, shock, and coupled acoustic-structural analysis.

The transient expressions for the coupled acoustic-structural problem are

\begin{matrix} \int_{V_{f}} [δ p (\frac{1}{K_{f}} \ddot{p} + \frac{r}{ρ_{f} K_{f}} \dot{p}) + & \frac{1}{ρ_{f}} \frac{\partial δ p}{\partial x} \cdot \frac{\partial p}{\partial x}] d V + \int ​_{S_{fs} \cup S_{frs}} δ p n ​^{-} \cdot \frac{\partial p}{\partial x} d S - \int ​_{S_{ft}} δ p a ​_{i n} d S \\ + \int_{S_{fr} \cup S_{frs}} δ p (\frac{r}{ρ_{f}} \frac{1}{c_{1}} p + (\frac{r}{ρ_{f}} \frac{1}{k_{1}} + \frac{1}{c_{1}}) \dot{p} + \frac{1}{k_{1}} \ddot{p}) d S = 0 \end{matrix}

(acoustic medium) and

\begin{matrix} \int_{V} δ ε : σ d V + \int_{V} α_{c} ρ δ u^{m} \cdot {\dot{u}}^{m} d V & + \int_{V} ρ δ u^{m} \cdot {\ddot{u}}^{m} d V \\ + \int_{S_{fs} \cup S_{frs}} δ u^{m} \cdot n^{-} p d S & - \int_{S_{t}} δ u^{m} \cdot t d S = 0 \end{matrix}

(structural medium), where $n^{-}$ is the normal vector pointing into the fluid. The fluid-solid surface consists of the union of the directly coupled fluid-solid region, $S_{fs}$ , and a region coupled via a “reactive” acoustic surface or impedance boundary, $S_{frs}$ . Of primary interest here are those terms integrated over $S_{fs} \cup S_{frs}$ , which couple the two variational equations. The fluid impedance integral, over $S_{fr} \cup S_{frs}$ , depends only on the acoustic pressure field and its variations, so it is unaffected by the contact with the solid. The derivation for the steady-state case is formally identical to the transient case and will not be discussed here. For details of the differences in transient and steady-state acoustics in Abaqus, see Coupled acoustic-structural medium analysis.

When ASIn elements are used (see Acoustic interface elements), the formulation requires that the fluid and solid elements be geometrically and nodally conformal so that the shape functions for the structural displacements and the acoustic pressures are identical. The shape functions are integrated using standard methods to yield element matrices of dimension equal to the number of surface nodes on the element. The complete fluid-solid coupling matrices are formed by the sum over the element faces; that is, a standard element assembly operation. The two final coupling matrices have the sparsity pattern of the coupled fluid-solid element faces.

In surface-based coupling the interaction surface $S_{fs} \cup S_{frs}$ is formed by the boundary between possibly nonconforming structural and acoustic meshes. Therefore, the fluid-solid coupling matrix cannot be broken up into a sum over element faces as simply as in the ASIn case. To derive the coupling matrices in the surface-based procedure, we use a variation of the master-slave procedure used in small-sliding contact (see Small-sliding interaction between bodies). At the start of an analysis, the projections $x_{N}$ of slave nodes onto the master surface are found, and the areas $A_{N}$ and normals $n^{-} (x_{N})$ associated with the slave nodes are computed. The projections are points $p (x_{N})$ on the master surface; master nodes in the vicinity of this projection are identified. Variables at the slave nodes $x_{N}$ are then interpolated from variables at the identified master surface nodes near the projection $p (x_{N})$ .

Since the physical degrees of freedom for the fluid and solid meshes are different, two cases must be treated. The two cases handle the discretization of the coupling terms differently.

Solid/structural master, fluid slave

If the fluid medium surface is designated as the slave, we constrain values at each fluid node to be an average of the values at nearby master surface nodes (see Figure 1). The pointwise fluid-solid coupling condition,

\frac{1}{ρ_{f}} \frac{\partial p}{\partial x} \cdot n^{-} + {\ddot{u}}^{m} \cdot n^{-} = 0,

is enforced at the slave nodes, resulting in displacement degrees of freedom added to the fluid slave surface. These slave displacements are constrained by the master displacements and thereby eliminated; the slave pressures are not constrained directly.

Figure 1. Fluid slave.

Hence, the fluid equation coupling term

\int_{S_{fs} \cup S_{frs}} δ p n^{-} \cdot \frac{\partial p}{\partial x} d S

is equal to

- \int_{S_{fs} \cup S_{frs}} δ p n^{-} \cdot {\ddot{u}}^{m} d S .

This term is now approximated, at the slave node level, by the interpolated values of structural displacements at the nearby master nodes times the area of the slave node:

\int_{S_{fs} \cup S_{frs}} δ p n^{-} \cdot {\ddot{u}}^{m} d S \approx A_{N} [\sum_{i} n^{-} (x_{N}) \cdot N^{i} (p (x_{N})) {\ddot{u}}_{i}^{m}],

where $N^{i} (p (x_{N}))$ is the master surface interpolant evaluated at the projection of the slave node, ${\ddot{u}}_{i}^{m}$ are the structural accelerations at the master nodes, and $n^{-} (x_{N})$ is the normal vector, pointing into the fluid, evaluated at the slave node. The summation extends over all master nodes $i$ in the vicinity of the slave node projection $p (x_{N})$ (see Figure 1). The computation is repeated for each slave node $x_{N}$ on the surface $S_{fs} \cup S_{frs}$ and assembled to form the entire coupling matrix.

Similarly, the contribution to the pressure coupling term in the structural equation due to slave node $x_{N}$ is approximated by

\int_{S_{fs} \cup S_{frs}} δ u^{m} \cdot n^{-} p d S \approx p_{N} A_{N} [\sum_{i} n^{-} (x_{N}) \cdot N^{i} (p (x_{N}))],

where $p_{N}$ is the acoustic pressure at slave node $x_{N}$ , and the sum is again over the master nodes $i$ in the vicinity of the slave node projection.

These expressions for the coupling terms result in matrices that are the transpose of each other. The normal vectors at the slave surface are used, so these vectors must be well-defined (see About surfaces).

Fluid master, solid/structural slave

If the solid medium is designated as the slave, the values on this surface are constrained to equal values interpolated from the master surface. The pointwise fluid-solid coupling condition is again enforced at the slave nodes, resulting in acoustic pressure degrees of freedom added to the solid slave surface (see Figure 2). These slave pressures are constrained by the master surface acoustic pressures and eliminated; the slave displacements are not constrained directly. Hence, the contribution to the coupling term in the acoustic equation for a single slave node $x_{N}$ is approximated by

\int_{S_{fs} \cup S_{frs}} δ p n^{-} \cdot {\ddot{u}}^{m} d S \approx [A_{N} n^{-} (x_{N}) \cdot {\ddot{u}}_{N}^{m}] [\sum_{i} H^{i} (p (x_{N}))],

where ${\ddot{u}}_{N}^{m}$ is the structural acceleration at the slave node and $H^{i} (p (x_{N}))$ are the interpolants on the fluid (master) surface evaluated at the projection $p (x_{N})$ . The summation extends over the master nodes $i$ in the vicinity of the slave node projection and is repeated for all solid/structural nodes in the surface $S_{fs} \cup S_{frs}$ to compute the entire coupling matrix.

Figure 2. Fluid master.

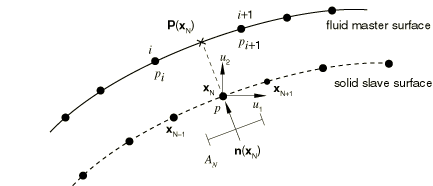
The contribution of a slave node to the coupling term in the structural equation is approximated by

\int_{S_{fs} \cup S_{frs}} δ u^{m} \cdot n^{-} p d S \approx A_{N} \sum_{i} H^{i} (p (x_{N})) p_{i},

where $p_{i}$ is the pressure at master node $i$ and the sum is again over the master nodes in the vicinity of the slave node projection $p (x_{N})$ .