Superelasticity

The superelastic model is based on the uniaxial stress-strain response of phase transforming materials (Figure 1). Such materials (e.g., Nitinol) are in the austenite phase under no loading conditions. Austenite is assumed to follow isotropic linear elasticity. On loading the material, the austenite phase starts transforming into martensite beyond a certain stress. Martensite is also assumed to follow isotropic linear elasticity. During the phase transformation, elastic properties are calculated from the elastic constants of austenite and martensite, following the rule of mixtures:

where $\zeta$ is the fraction of martensite, $E_A$ is the Young's modulus of austenite, $E_M$ is the Young's modulus of martensite, ${\nu }_A$ is the Poisson's ratio of austenite, and ${\nu }_M$ is the Poisson's ratio of martensite. After a certain stress, austenite is completely transformed into martensite, which deforms elastically thereafter. Therefore, the deformation follows the elastic constants of austenite when the fraction of martensite is zero and follows the elastic constants of martensite if the fraction of martensite is one (full transformation). On unloading, martensite transforms back into austenite and the transformation strain is fully recovered. However, the stress at which the reverse transformation occurs is different from the stress at which the austenite to martensite transformation occurred.

Figure 1. Uniaxial response of a superelastic material.

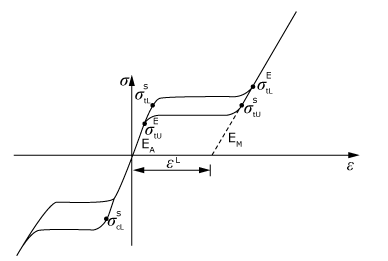
In this model the total strain increment, $\mathrm{\Delta }\epsilon$, is assumed to be the sum of the elastic strain increment, $\mathrm{\Delta }{\epsilon }^{el}$, and the increment in transformation strain, $\mathrm{\Delta }{\epsilon }^{tr}$:

The increment in transformation strain is calculated using the following flow rule:

where $G^{tr}$ is the transformation flow potential. The transformation potential is assumed to follow the Drucker-Prager form:

where $p=-\frac{1}{3}\mathrm{trace}\sigma$ is the equivalent pressure stress, and $q=\sqrt{\frac{3}{2}S:S}$ is the Mises equivalent stress.

The transformation surface, $F^{tr}$, is also assumed to follow the Drucker-Prager form, and it varies linearly with temperature, $T$:

In the case of tensile loading, $F^{tr}$ should lie between ${\sigma }_{tL}^S$ and ${\sigma }_{tL}^E$; during unloading, $F^{tr}$ should be between ${\sigma }_{tU}^S$ and ${\sigma }_{tU}^E$. A difference in the response of the specimen during loading in tension and compression can be obtained by specifying a value of ${\sigma }_{cL}^S$, which is different from ${\sigma }_{tL}^S$. The angles $\beta$ and $\psi$ are calculated from the tensile and compressive transformation stress levels, the uniaxial transformation strain, and the volumetric transformation strain provided by the user.

You can specify the stress levels at which the transformation takes place at the reference temperature, $T_0$. These stress levels are assumed to vary linearly with temperature, as shown in Figure 2.

The material data cannot be specified as a function of temperature or field variables.

Figure 2. Stress vs. temperature curve.

You can define the Young's modulus and Poisson's ratio of austenite.

ELASTIC

Property module: material editor: MechanicalElasticity: Elastic

You can define the elastic properties of martensite, the critical stress levels for forward and reverse transformation, and the variation of transformation plateau with temperature.

SUPERELASTIC

Property module: material editor: MechanicalSuperelasticity

Shape setting is done by setting all the state variables to zero. The procedure varies between Abaqus/Standard and Abaqus/Explicit. In Abaqus/Standard you must remove and reactivate elements. In Abaqus/Explicit you only need to specify the annealing process.

SUPERELASTIC
MODEL CHANGE, REMOVE
MODEL CHANGE, ADD=STRAIN FREE

SUPERELASTIC
ANNEAL

Property module: material editor: MechanicalSuperelasticity
Interaction module: Create Interaction: Model Change: Definition: Region, Activation state of region elements: Deactivated in this step
Interaction module: Create Interaction: Model Change: Definition: Region, Activation state of region elements: Reactivated in this step

Property module: material editor: MechanicalSuperelasticity
Step module: Create Step: General: Anneal