Permanent set in rubberlike materials

The real behavior of filled rubber elastomers under cyclic loading conditions is quite complex as shown in Figure 1.

Figure 1. Typical behavior of a filled elastomer.

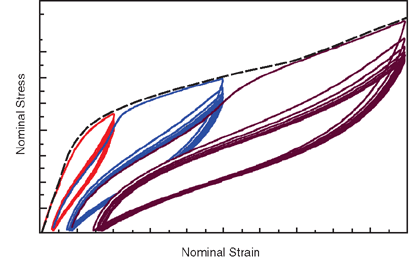
The observed mechanical behaviors are progressive damage resulting in a reduction of load-carrying capacity with each cycle, stress softening (also known as Mullins effect) upon reloading after the first unloading from a previously attained maximum strain level, hysteretic dissipation of energy, and permanent set. This section is concerned with modeling permanent set; therefore, the idealized representation of permanent set is described below.

The primary hyperelastic behavior can be defined by using any of the hyperelastic material models (see Hyperelastic behavior of rubberlike materials). If test data input is used to define the hyperelastic response of the material, the data must be specified with respect to the stress-free intermediate configuration after unloading has taken place.

Permanent set can be defined through an isotropic hardening function in terms of the yield stress and the equivalent plastic strain. In this case the yield stress is the (effective) Kirchoff stress on the primary loading path from which unloading takes place, and the equivalent plastic strain is the corresponding logarithmic permanent set observed in the material. If $\sigma$ is the true (Cauchy) stress, Kirchoff stress is defined as $J\sigma$, where $J$ is the determinant of $\mathbf{F}$.

Depending on what is being modeled, permanent set may be defined as the true permanent set seen in the material after recovery of viscoelastic strains or it may include viscoelastic strains. In either case, an initial yield stress is required, below which there will be no permanent set and the behavior of the material will be fully elastic. In the case of filled rubbers this initial yield stress may correspond to a small nonzero stress; whereas for the family of thermoplastic materials, there may be a more marked value of initial yield stress.

PLASTIC, HARDENING=ISOTROPIC

Property module: material editor: MechanicalPlasticityPlastic

The model is intended to capture permanent set under multiaxial stress states and mild reverse loading conditions, as illustrated by Govindarajan, Hurtado, and Mars (2007). This model is not intended to capture deformation under complete reverse loading. Any rate effects apply only to the plastic part of the material definition.