Structural problems | ||
| ||
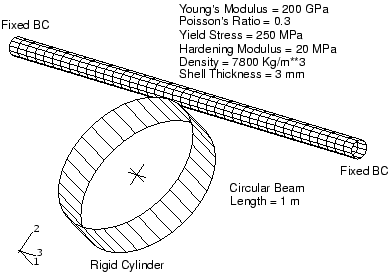
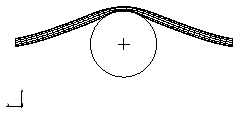
The response of the beam varies greatly with the loading rate. At an extremely high impact velocity of 400 m/s, the deformation in the beam is highly localized, as shown in Figure 2. To obtain a better quasi-static solution, consider the lowest mode.
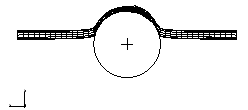
The frequency of the lowest mode is approximately 250 Hz, which corresponds to a period of 4 milliseconds. The natural frequencies can be calculated easily using the eigenfrequency extraction procedure in Abaqus/Standard. To deform the beam by the desired 0.2 m in 4 milliseconds, the velocity of the cylinder is 50 m/s. While 50 m/s still seems like a high impact velocity, the inertial forces become secondary to the overall stiffness of the structure, and the deformed shape—shown in Figure 3—indicates a much better quasi-static response. While the overall structural response appears to be what we expect as a quasi-static solution, it is usually desirable to increase the loading time to 10 times the period of the lowest mode to be certain that the solution is truly quasi-static. To improve the results even further, the velocity of the rigid cylinder could be ramped up gradually—for example, using a smooth step amplitude curve—thereby easing the initial impact.