Bulk viscosity | ||
| ||
- Linear bulk viscosity
By default, linear bulk viscosity is always included to damp “ringing” in the highest element frequency. It generates a bulk viscosity pressure that is linear in the volumetric strain rate, according to the following equation:
where is a damping coefficient, whose default value is 0.06, is the current material density, is the current dilatational wave speed, is the element characteristic length, and is the volumetric strain rate.
- Quadratic bulk viscosity
Quadratic bulk viscosity is included only in continuum elements (except for the plane stress element, CPS4R) and is applied only if the volumetric strain rate is compressive. The bulk viscosity pressure is quadratic in the strain rate, according to the following equation:
where is the damping coefficient, whose default value is 1.2.
The quadratic bulk viscosity smears a shock front across several elements and is introduced to prevent elements from collapsing under extremely high velocity gradients. Consider a simple one-element problem in which the nodes on one side of the element are fixed and the nodes on the other side have an initial velocity in the direction of the fixed nodes, as shown in Figure 1.
Figure 1. Element with fixed nodes and prescribed velocities.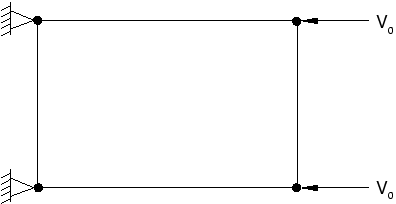
The stable time increment size is precisely the transit time of a dilatational wave across the element. Therefore, if the initial nodal velocity is equal to the dilatational wave speed of the material, the element collapses to zero volume in one time increment. The quadratic bulk viscosity pressure introduces a resisting pressure that prevents the element from collapsing.
- Fraction of critical damping due to bulk viscosity
The bulk viscosity pressures are based on only the dilatational modes of each element. The fraction of critical damping in the highest element mode is given by the following equation:
where is the fraction of critical damping. The linear term alone represents 6% of critical damping, whereas the quadratic term is usually much smaller.