Defining hyperelastic behavior using test data | ||
| ||
-
Uniaxial tension and compression
-
Equibiaxial tension and compression
-
Planar tension and compression (pure shear)
-
Volumetric tension and compression
The deformation modes seen in these tests are shown in Figure 1.
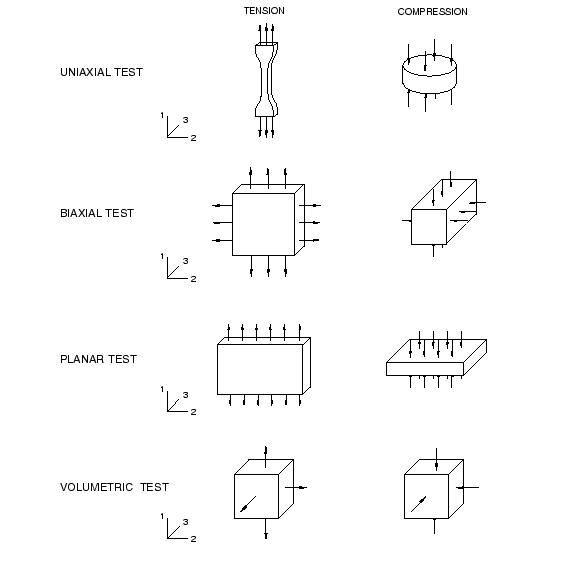
Unlike plasticity data, the test data for hyperelastic materials must be given to Abaqus as nominal stress and nominal strain values.
Volumetric compression data only need to be given if the material's compressibility is important. Normally in Abaqus/Standard it is not important, and the default fully incompressible behavior is used. As noted earlier, Abaqus/Explicit assumes a small amount of compressibility if no volumetric test data are given.
- Obtaining the best material model from your data
-
The quality of the results from a simulation using hyperelastic materials strongly depends on the material test data that you provide Abaqus. Typical tests are shown in Figure 1. There are several things that you can do to help Abaqus calculate the best possible material parameters.
Wherever possible, try to obtain experimental test data from more than one deformation state—this allows Abaqus to form a more accurate and stable material model. However, some of the tests shown in Figure 1 produce equivalent deformation modes for incompressible materials. The following are equivalent tests for incompressible materials:
-
Uniaxial tension ↔ Equibiaxial compression
-
Uniaxial compression ↔ Equibiaxial tension
-
Planar tension ↔ Planar compression
You do not need to include data from a particular test if you already have data from another test that models a particular deformation mode.
In addition, the following may improve your hyperelastic material model:
-
Obtain test data for the deformation modes that are likely to occur in your simulation. For example, if your component is loaded in compression, make sure that your test data include compressive, rather than tensile, loading.
-
Both tension and compression data are allowed, with compressive stresses and strains entered as negative values. If possible, use compression or tension data depending on the application, since the fit of a single material model to both tensile and compressive data will normally be less accurate than for each individual test.
-
Try to include test data from the planar test. This test measures shear behavior, which can be very important.
-
Provide more data at the strain magnitudes that you expect the material will be subjected to during the simulation. For example, if the material will only have small tensile strains, say under 50%, do not provide much, if any, test data at high strain values (over 100%).
-
Use the material evaluation functionality in Abaqus/CAE to perform simulations of the experimental tests and to compare the results Abaqus calculates to the experimental data. If the computational results are poor for a particular deformation mode that is important to you, try to obtain more experimental data for that deformation mode. The technique is illustrated as part of the example discussed in Example: axisymmetric mount. Please consult the Abaqus/CAE User's Guide for further details.
-
- Stability of the material model
-
It is common for the hyperelastic material model determined from the test data to be unstable at certain strain magnitudes. Abaqus performs a stability check to determine the strain magnitudes where unstable behavior will occur and prints a warning message in the data (.dat) file. The same information is printed in the Material Parameters and Stability Limit Information dialog box that appears when the material evaluation capability is used in Abaqus/CAE. You should check this information carefully since your simulation may not be realistic if any part of the model experiences strains beyond the stability limits. The stability checks are done for specific deformations, so it is possible for the material to be unstable below the strain levels indicated if the deformation is more complex. In Abaqus/Standard your simulation may not converge if a part of the model exceeds the stability limits.
See Hyperelastic behavior of rubberlike materials for suggestions on improving the accuracy and stability of the test data fit.