Characterizing elements | ||
| ||
-
Family
-
Degrees of freedom (directly related to the element family)
-
Number of nodes
-
Formulation
-
Integration
Each element in Abaqus has a unique name, such as T2D2, S4R, or C3D8I. The element name identifies each of the five aspects of an element. The naming convention is explained in this chapter.
- Family
-
Figure 1 shows the element families most commonly used in a stress analysis. One of the major distinctions between different element families is the geometry type that each family assumes.
Figure 1. Commonly used element families.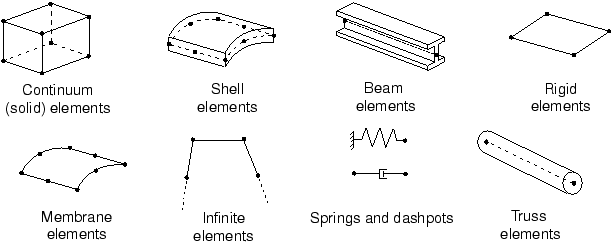
The element families that you will use in this guide—continuum, shell, beam, truss, and rigid elements—are discussed in detail in other chapters. The other element families are not covered in this guide; if you are interested in using them in your models, read about them in Abaqus Elements Guide.
The first letter or letters of an element's name indicate to which family the element belongs. For example, the S in S4R indicates this is a shell element, while the C in C3D8I indicates this is a continuum element.
- Degrees of freedom
-
The degrees of freedom (dof) are the fundamental variables calculated during the analysis. For a stress/displacement simulation the degrees of freedom are the translations at each node. Some element families, such as the beam and shell families, have rotational degrees of freedom as well. For a heat transfer simulation the degrees of freedom are the temperatures at each node; a heat transfer analysis, therefore, requires the use of different elements than a stress analysis, since the degrees of freedom are not the same.
The following numbering convention is used for the degrees of freedom in Abaqus:
1 Translation in direction 1 2 Translation in direction 2 3 Translation in direction 3 4 Rotation about the 1-axis 5 Rotation about the 2-axis 6 Rotation about the 3-axis 7 Warping in open-section beam elements 8 Acoustic pressure, pore pressure, or hydrostatic fluid pressure 9 Electric potential 10 Connector material flow (units of length) 11 Temperature (or normalized concentration in mass diffusion analysis) for continuum elements or temperature at the first point through the thickness of beams and shells 12+ Temperature at other points through the thickness of beams and shells Directions 1, 2, and 3 correspond to the global 1-, 2-, and 3-directions, respectively, unless a local coordinate system has been defined at the nodes.
Axisymmetric elements are the exception, with the displacement and rotation degrees of freedom referred to as follows:
1 Translation in the r-direction 2 Translation in the z-direction 6 Rotation in the r–z plane Directions r (radial) and z (axial) correspond to the global 1- and 2-directions, respectively, unless a local coordinate system has been defined at the nodes. See Using Shell Elements for a discussion of defining a local coordinate system at the nodes.
In this guide our attention is restricted to structural applications. Therefore, only elements with translational and rotational degrees of freedom are discussed. For information on other types of elements (for example, heat transfer elements), consult the Abaqus Elements Guide.
By default, Abaqus/CAE uses the alphabetical option, x-y-z, for labeling the view orientation triad. In general, this guide adopts the numerical option, 1-2-3, to permit direct correspondence with degree of freedom and output labeling. For more information on labeling of axes, see Customizing the view triad.
- Number of nodes—order of interpolation
-
Displacements, rotations, temperatures, and the other degrees of freedom mentioned in the previous section are calculated only at the nodes of the element. At any other point in the element, the displacements are obtained by interpolating from the nodal displacements. Usually the interpolation order is determined by the number of nodes used in the element, as illustrated in the examples in Figure 2.
Figure 2. Linear brick, quadratic brick, and modified tetrahedral elements.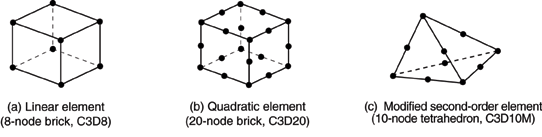
-
Elements that have nodes only at their corners, such as the 8-node brick shown in Figure 2(a), use linear interpolation in each direction and are often called linear elements or first-order elements.
-
Elements with midside nodes, such as the 20-node brick shown in Figure 2(b), use quadratic interpolation and are often called quadratic elements or second-order elements.
-
Modified triangular or tetrahedral elements with midside nodes, such as the 10-node tetrahedron shown in Figure 2(c), use a modified second-order interpolation and are often called modified elements or modified second-order elements.
Abaqus/Standard offers a wide selection of both linear and quadratic elements. Abaqus/Explicit offers only linear elements, with the exception of the quadratic beam and modified tetrahedron and triangle elements.
Typically, the number of nodes in an element is clearly identified in its name. The 8-node brick element, as you have seen, is called C3D8; and the 8-node general shell element is called S8R. The beam element family uses a slightly different convention: the order of interpolation is identified in the name. Thus, a first-order, three-dimensional beam element is called B31, whereas a second-order, three-dimensional beam element is called B32. A similar convention is used for axisymmetric shell and membrane elements.
-
- Formulation
-
An element's formulation refers to the mathematical theory used to define the element's behavior. In the absence of adaptive meshing all of the stress/displacement elements in Abaqus are based on the Lagrangian or material description of behavior: the material associated with an element remains associated with the element throughout the analysis, and material cannot flow across element boundaries. In the alternative Eulerian or spatial description, elements are fixed in space as the material flows through them. Eulerian methods are used commonly in fluid mechanics simulations. Abaqus/Standard uses Eulerian elements to model convective heat transfer. Adaptive meshing combines the features of pure Lagrangian and Eulerian analyses and allows the motion of the element to be independent of the material. Eulerian elements and adaptive meshing are not discussed in this guide.
To accommodate different types of behavior, some element families in Abaqus include elements with several different formulations. For example, the shell element family has three classes: one suitable for general-purpose shell analysis, another for thin shells, and yet another for thick shells. (These shell element formulations are explained in Using Shell Elements.)
Some Abaqus/Standard element families have a standard formulation as well as some alternative formulations. Elements with alternative formulations are identified by an additional character at the end of the element name. For example, the continuum, beam, and truss element families include members with a hybrid formulation in which the pressure (continuum elements) or axial force (beam and truss elements) is treated as an additional unknown; these elements are identified by the letter “H” at the end of the name (C3D8H or B31H).
Some element formulations allow coupled field problems to be solved. For example, elements whose names begin with the letter C and end with the letter T (such as C3D8T) possess both mechanical and thermal degrees of freedom and are intended for coupled thermomechanical simulations.
Several of the most commonly used element formulations are discussed later in this guide.
- Integration
-
Abaqus uses numerical techniques to integrate various quantities over the volume of each element. Using Gaussian quadrature for most elements, Abaqus evaluates the material response at each integration point in each element. Some elements in Abaqus can use full or reduced integration, a choice that can have a significant effect on the accuracy of the element for a given problem, as discussed in detail in Element formulation and integration.
Abaqus uses the letter “R” at the end of the element name to distinguish reduced-integration elements (unless they are also hybrid elements, in which case the element name ends with the letters “RH”). For example, CAX4 is the 4-node, fully integrated, linear, axisymmetric solid element; and CAX4R is the reduced-integration version of the same element.
Abaqus/Standard offers both full and reduced-integration elements; Abaqus/Explicit offers only reduced-integration elements with the exception of the modified tetrahedron and triangle elements and the fully integrated first-order shell, membrane, and brick elements.