Natural frequencies and mode shapes

Figure 1. Mass-spring system.

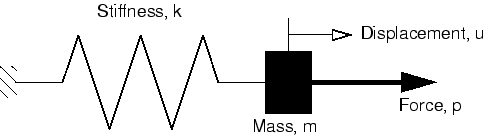
The internal force in the spring is given by $k u$ so that its dynamic equation of motion is

m \ddot{u} + k u - p = 0.

This mass-spring system has a natural frequency (in radians/time) given by

ω = \sqrt{\frac{k}{m}} .

If the mass is moved and then released, it will oscillate at this frequency. If the force is applied at this frequency, the amplitude of the displacement will increase dramatically—a phenomenon known as resonance.

Real structures have a large number of natural frequencies. It is important to design structures in such a way that the frequencies at which they may be loaded are not close to the natural frequencies. The natural frequencies can be determined by considering the dynamic response of the unloaded structure ( $P = 0$ in the dynamic equilibrium equation). The equation of motion is then

M \ddot{u} + I = 0.

For an undamped system $I = K u$ , so

M \ddot{u} + K u = 0.

Solutions to this equation have the form

u = ϕ e^{i ω t} .

Substituting this into the equation of motion yields the eigenvalue problem

K ϕ = λ M ϕ,

where $λ = ω^{2}$ .

This system has n eigenvalues, where n is the number of degrees of freedom in the finite element model. Let $λ_{j}$ be the jth eigenvalue. Its square root, $ω_{j}$ , is the natural frequency of the jth mode of the structure, and $ϕ_{j}$ is the corresponding jth eigenvector. The eigenvector is also known as the mode shape because it is the deformed shape of the structure as it vibrates in the jth mode.

The frequency extraction procedure in Abaqus/Standard is used to determine the modes and frequencies of the structure. This procedure is easy to use in that you need only specify the number of modes required or the maximum frequency of interest.