Shear deformation | ||
| ||
Abaqus assumes the transverse shear stiffness of these beam elements to be linear elastic and constant. In addition, these beams are formulated so that their cross-sectional area can change as a function of the axial deformation, an effect that is considered only in geometrically nonlinear simulations (see Nonlinearity) in which the section Poisson's ratio has a nonzero value. These elements can provide useful results as long as the cross-section dimensions are less than 1/10 of the typical axial dimensions of the structure, which is generally considered to be the limit of the applicability of beam theory; if the beam cross-section does not remain plane under bending deformation, beam theory is not adequate to model the deformation.
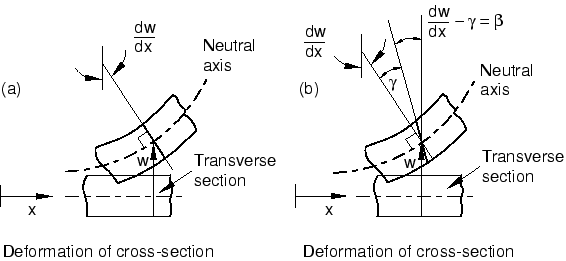
The cubic elements available in Abaqus/Standard—the so-called Euler-Bernoulli beam elements (B23 and B33)—do not model shear flexibility. The cross-sections of these elements remain perpendicular to the beam axis (see Figure 1(a)). Therefore, the cubic beam elements are most effective for modeling structures with relatively slender members. Since cubic elements model a cubic variation of displacement along their lengths, a structural member often can be modeled with a single cubic element for a static analysis and with a small number of elements for a dynamic analysis. These elements assume that shear deformations are negligible. Generally, if the cross-section dimensions are less than 1/15 of the typical axial dimensions of the structure, this assumption is valid.