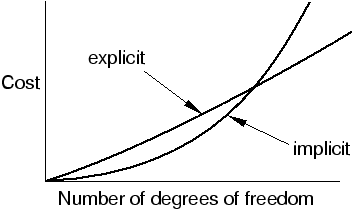
Cost of mesh refinement in implicit and explicit analyses

Whereas predicting the cost increase with mesh refinement for the explicit method is rather straightforward, cost is more difficult to predict when using the implicit method. The difficulty arises from the problem-dependent relationship between element connectivity and solution cost, a relationship that does not exist in the explicit method. Using the implicit method, experience shows that for many problems the computational cost is roughly proportional to the square of the number of degrees of freedom. Consider the same example of a three-dimensional model with uniform, square elements. Refining the mesh by a factor of two in all three directions increases the number of degrees of freedom by approximately 2³, causing the computational cost to increase by a factor of roughly (2³)², or 64. The disk space and memory requirements increase in the same manner, although the actual increase is difficult to predict.

The explicit method shows great cost savings over the implicit method as the model size increases, as long as the mesh is relatively uniform. Figure 1 illustrates the comparison of cost versus model size using the explicit and implicit methods. For this problem the number of degrees of freedom scales with the number of elements.