Mixing of granular media in a drum mixer

This example demonstrates using the discrete element method (DEM) in Abaqus to analyze mixing of different particulate media in a tumbling mill.

The following topics are discussed:

Application description
Abaqus modeling approaches and simulation techniques
Case 1 Nonadhesive contact between limestone pellets
Case 2 Adhesive contact between polyethylene pellets
Discussion of results and comparison of cases
Input files
References
Figures

Application description

Rotating drum mixers and tumbling mills are used for grinding, mixing, and drying of ore and granular materials. Such applications can be found in a wide range of industrial sectors such as mining. Several factors (including shape, size, density, and contact stiffness of particles; friction; adhesion between particles, speed of rotation; and tilt of the drum axis) influence the level of mixing that will be achieved in a given amount of time. These factors also influence the amount of energy required to operate the mixer. The discrete element method (DEM) is a useful tool in understanding the effects of these factors on the mixing process. This example demonstrates the use of DEM to analyze mixing of granular media with nonadhesive as well as adhesive contact behavior.

Geometry

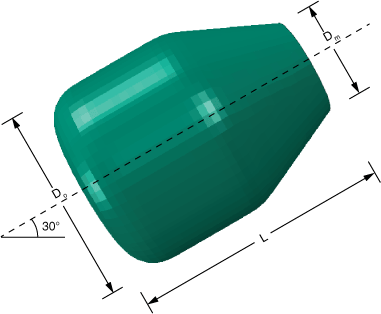
Figure 1 shows the drum geometry. The drum length, L, is 760 mm; the drum outer diameter, $D_{o}$ , is 620 mm; and the drum mouth diameter, $D_{m}$ , is 315 mm. The interior of the drum has five equally spaced baffles to aid the mixing process. The baffles taper from the rear to the front of the drum. The wall of the drum is hollow; and the drum inner radius, R, is 300 mm. The axis of the drum is inclined at an angle of 30°. Although this laboratory size drum mixer is not of the scale of an industrial mixer, it is sufficiently large to demonstrate the mixing process.

To analyze nonadhesive contact between particles, the granular media consist of two batches of spherical limestone pellets. The first batch has a mass of 16.3 kg, and each pellet has a radius of 5 mm. The second batch has a mass of 19.3 kg, and each pellet has a radius of 6 mm. To analyze adhesive contact between particles, the granular media consist of two batches of spherical polyethylene pellets. The first batch has a mass of 9.8 kg, and each pellet has a radius of 5 mm. The second batch has a mass of 11.2 kg, and each pellet has a radius of 6 mm.

Materials

The drum is made of steel with a Young's modulus of 2.08 × 10⁵ N/mm², density of 7850 × 10^–9 kg/mm³, and Poisson's ratio of 0.3.

Boundary conditions and loading

Mixing of particles in a rotating drum is influenced by the drum radius, the speed of rotation, and the degree of filling of the drum. At slow rotating speeds, particles tend to slip and slump along the walls of the drum; while at very high speeds, centrifuging occurs, pushing the particles up along the drum wall. Rolling and cascading of particles in a rotating drum results in good mixing. The Froude number specifies the tendency of the particles to roll and cascade during mixing in a rotating drum. The Froude number is defined as $ω^{2} R / g$ , where $ω$ is the angular speed of the drum, R is the drum radius, and g is the acceleration due to gravity. A Froude number in the range of 0.001–0.1 is recommended for mixing operations. In this example the reference node of the drum is given a rotating speed of slightly less than 0.25 revolutions per second, which results in a Froude number of 0.068. The two batches of pellets together occupy less than half of the interior volume of the drum (i.e., the degree of filling is less than 0.5). The entire model in this example is subjected to gravity loading.

Interactions

Two different contact conditions between particles are considered: nonadhesive contact between limestone pellets, and adhesive contact between polyethylene pellets. Contact between particles and the drum is nonadhesive. The friction coefficient for contact between particles is 0.35. For contact between particles and the drum wall, the friction coefficient is 0.3.

Abaqus modeling approaches and simulation techniques

For this analysis the drum is assumed to be a rigid body. It is meshed with shell elements and made rigid by assigning it to a rigid body. A CARDAN connection type connector element that is aligned with the drum axis is attached to the reference node of the drum. The connector element is used to apply the torque to rotate the drum. The limestone and polyethylene pellets are modeled using PD3D elements. The particles are spherical in shape. The model used in this example has 8556 PD3D elements with a 6 mm radius and 12478 PD3D elements with a 5 mm radius.

Summary of analysis cases

Case 1	Nonadhesive contact between limestone pellets.
Case 2	Adhesive contact between polyethylene pellets.

Mesh design

It is very difficult to start such a simulation with the particles positioned precisely in an equilibrated configuration. A common DEM modeling technique is used for this analysis in which arrays of particles are initially positioned in the model and allowed to settle under gravity during the first analysis step with no other loading. The desired loading response is studied in subsequent steps.

In this case, layers of nonoverlapping particles of both sizes are introduced inside the drum. The two batches of particles are initially positioned next to each other and at a certain initial height from the interior wall of the drum. Next, these two batches of particles are dropped inside the drum and allowed to settle under gravity. This is done via a dummy step of 0.5 seconds duration in which only the gravity load is active. The drum is held fixed in its initial position during this step. At the end of the gravity settling step, we have the two batches of particles in a compacted stable configuration at the lower part of the drum. The cost of gravity settling is an additional overhead incurred in most DEM analyses.

Boundary conditions

An encastre boundary condition is applied to the free end of the connector, and all translational degrees of freedom of the reference point of the rigid body are held fixed for the duration of the analysis.

Loads

A gravity load is applied to the model. An acceleration of −9800 mm/s² is applied in the z-direction. Velocity type connector motion with an amplitude is applied about the connector component aligned with the drum axis. The other two connector components are held fixed. Mass proportional damping is used in the analysis to reduce the analysis noise. The total time period for the analysis, which includes gravity settling and mixing, is 5.5 seconds.

Case 1 Nonadhesive contact between limestone pellets

Two batches of spherical limestone pellets are used to analyze nonadhesive contact between particles.

Materials

Limestone has a Young's modulus of 2.0 × 10⁴ N/mm², density of 2500 × 10^–9 kg/mm³, and Poisson's ratio of 0.25.

Interactions

As discussed in Discrete element method, PD3D elements are rigid and the contact stiffness for interactions between DEM particles can be tuned to reflect the Hertz contact solution for contact between two elastic spheres (see Timoshenko and Goodier, 1951; and The Hertz contact problem). The Hertz solution relating the contact force, F, to the approach distance, $δ$ , between remote points on two contacting spheres is

F = \frac{4}{3} E^{*} \sqrt{R} \sqrt{δ^{3}},

where

R = \frac{R_{1} R_{2}}{R_{1} + R_{2}},

and

\frac{1}{E^{*}} = \frac{1 - ν_{1}^{2}}{E_{1}} + \frac{1 - ν_{2}^{2}}{E_{2}} .

$E_{1}$ , $ν_{1}$ and $E_{2}$ , $ν_{2}$ are the Young's modulus and Poisson's ratio of the two particles, respectively. $R_{1}$ and $R_{2}$ are the radii of the two particles, respectively.

The equation relating F and $δ$ was used to generate tabular force versus overclosure relationships for contact between DEM particles. Different relationships are used for different combinations of particle radii. In Abaqus force-overclosure tables are specified under tabular type pressure-overclosure contact surface behavior since the particle contact area is unity.

A simpler alternative is to specify an approximate linear contact stiffness over the range of $δ$ of interest. The Hertz contact stiffness is not linear because F is not linearly dependent on $δ$ . The normal contact stiffness (or slope of the F vs. $δ$ curve) for a given value of indentation between particles is

K = \frac{d F}{d δ} = 2 E^{*} \sqrt{R} \sqrt{δ} .

In Abaqus the contact stiffness can be specified using a linear type pressure-overclosure contact surface behavior. The maximum indentation $δ_{m a x}$ can be assumed to be a certain percentage of the particle radius (between 0.05 and 1.0 percent). Substituting a value such as $δ = 0.002$ into the expression for K may provide a linear contact stiffness that is adequately representative. For a given particle mass, a larger contact stiffness would require a smaller time increment. For a slow mixing process (i.e., the Froude number is at the low end of the mixing operation range), it may be possible to get reasonably accurate results with a lower contact stiffness and using larger time increments.

Case 2 Adhesive contact between polyethylene pellets

Two batches of spherical polyethylene pellets are used to analyze adhesive contact between particles.

Materials

Polyethylene has a Young's modulus of 1.0 × 10³ N/mm², density of 1400 × 10^–9 kg/mm³, and Poisson's ratio of 0.3.

Interactions

The Johnson-Kendall-Roberts (JKR) adhesive contact model discussed in Discrete element method is used for modeling adhesive contact between PD3D elements. The surface energy per unit area, $Γ$ , is used to specify adhesion between contacting particles; in this case, $Γ$ = 50 J/m². Increasing the value of $Γ$ leads to stronger adhesive forces between particles. The JKR model reduces to nonadhesive Hertz contact for $Γ = 0$ . Nonadhesive contact between polyethylene pellets is modeled ( $Γ$ = 0 J/m²) for comparison with adhesive contact results.

Discussion of results and comparison of cases

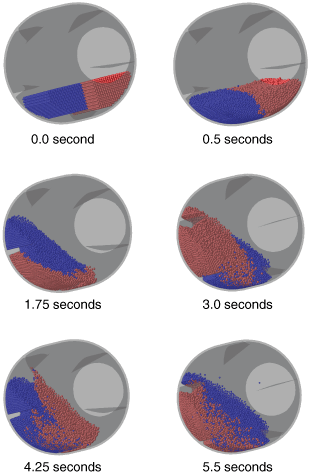
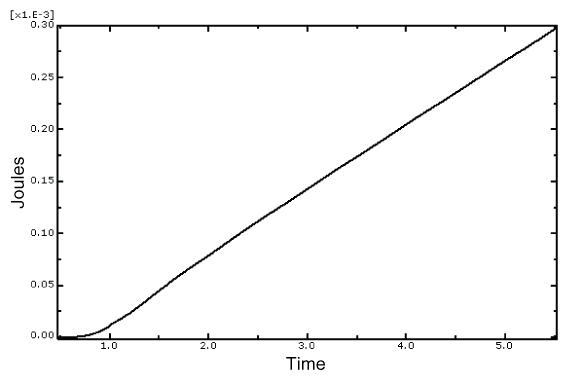
Figure 2 shows a series of deformed plots obtained at different times during the mixing analysis of limestone pellets. The initially generated mesh can be seen in the plot at 0.0 seconds. The configuration at the end of the gravity settling step can be seen in the plot at 0.5 seconds. The remaining four plots show the progress of the mixing process and the rolling and cascading of the particulate media. Figure 3 shows the total energy input to the mixing process as a function of time.

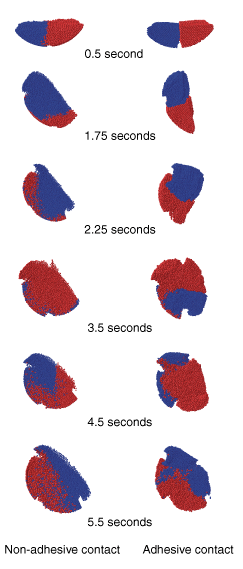
Figure 4 shows a comparison of the mixing process between the nonadhesive and adhesive mixing of polyethylene pellets. A series of deformed plots obtained at different times during the mixing analysis for the two conditions are juxtaposed in the figure. The steel drum has been removed from the plots for clarity. The left column of plots in Figure 4 corresponds to nonadhesive contact, and the right column of deformed plots corresponds to adhesive contact. The configuration at the end of the gravity settling step can be seen in the plot at 0.5 seconds. The remaining five plots show the progress of the mixing process. As can be seen from the figure, adhesion reduces the level of mixing. Also, the rolling and cascading of the particulate media that is observed in the modeling of nonadhesive contact for the polyethylene pellets is absent for adhesive contact.

Input files

Case 1

rotating_drum_mixer.inp: DEM nonadhesive drum mixing analysis using limestone pellets.
dem_drummixer_generator_2s_autodt.inp: DEM nonadhesive drum mixing analysis with particle generator and automatic time incrementation.

Case 2

rotating_drum_mixer_jkr.inp: DEM adhesive drum mixing analysis using polyethylene pellets.

References

Timoshenko, S., and J. N. Goodier,Theory of Elasticity, Second edition, McGraw-Hill, New York, 1951.

Figures

Figure 1. Mixer dimensions.

Figure 2. Case 1: Snapshots of the mixing process for limestone pellets.

Figure 3. Case 1: Energy input to the drum mixer.

Figure 4. Case 2: Comparison of the mixing process for nonadhesive and adhesive contact between particles.