Free meshing with quadrilateral and quadrilateral-dominated elements | ||
| ||
Abaqus/CAE allows you to choose between two meshing algorithms when you create a quadrilateral or quadrilateral-dominated mesh. For more information, see What is the difference between the medial axis algorithm and the advancing front algorithm?.
- Medial axis
-
When you free mesh a complex region with quadrilateral elements using the medial axis algorithm, Abaqus/CAE creates internal partitions that divide the region into simple structured mesh regions and then seeds the smaller regions.
If you use the medial axis algorithm to mesh a region and then remesh the region (for example, after modifying the seeds), Abaqus/CAE stores the internal partitions, and the new mesh is generated more quickly. In addition, the internal partitions allow Abaqus/CAE to generate a fine mesh in a similar time to that required to generate a coarse mesh. You cannot use the medial axis algorithm to mesh regions that contain virtual topology, and it does not work well with imprecise parts.
In general, a medial axis-based free mesh with quadrilateral elements does not match the mesh seeds exactly for the following reasons:
-
Abaqus/CAE tries to balance the seeds between adjacent regions and the smaller regions created by the internal partitioning.
-
Abaqus/CAE tries to minimize element distortions.
However, when you apply fixed seed constraints, Abaqus/CAE matches the number of seeds exactly and attempts to match the seed positions exactly. Figure 2 illustrates a two-dimensional plate with fixed seeds and movable seeds and the resulting all quadrilateral mesh.
Figure 2. Fixed and movable seeds and the medial axis meshing algorithm.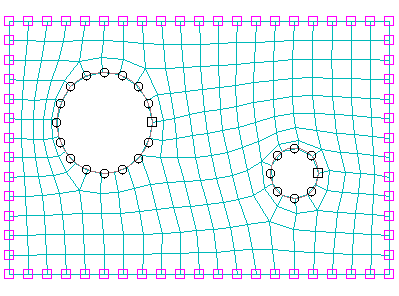
You should specify fixed seeds on only a few edges, or Abaqus/CAE may not be able to generate a mesh. For example, if you specify fixed seeds around one of the holes in the plate shown in Figure 2, the global seeding becomes overconstrained, and Abaqus/CAE cannot generate a mesh.
Using the medial axis algorithm, a free mesh generated with quadrilateral-dominated elements is similar to a free mesh generated with all quadrilateral elements and without transition minimization; however, Abaqus/CAE inserts a few isolated triangles in an effort to match the mesh seeds more closely. Abaqus/CAE can generate a mesh with quadrilateral-dominated elements faster than it can generate a mesh with all quadrilateral elements.
-
- Advancing front
-
When you free mesh a complex region with quadrilateral elements using the advancing front algorithm, Abaqus/CAE generates quadrilateral elements at the boundary of the region and continues to generate quadrilateral elements as it moves systematically to the interior of the region.
When you choose the advancing front algorithm, Abaqus/CAE matches the seeds exactly (except when you are creating a three-dimensional revolved mesh, and the profile being revolved touches the axis of revolution). A quadrilateral mesh that matches the seeds exactly is shown in Figure 3.
Figure 3. Fixed and movable seeds and the advancing front meshing algorithm.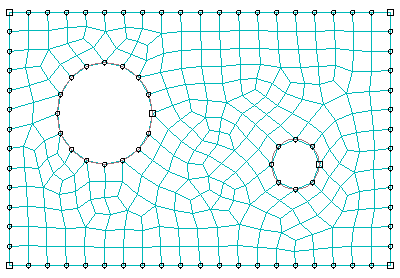
In general, the mesh transitions generated with the advancing front algorithm are more acceptable than the transitions generated by the medial axis algorithm; however, matching the seeds exactly in narrow regions may compromise the mesh quality. In contrast with the medial axis algorithm, you can use the advancing front algorithm in conjunction with imprecise parts and on regions that contain virtual topology.
If you select the advancing front algorithm, Abaqus/CAE will also use mapped meshing where appropriate. (Mapped meshing is the same as structured meshing but applies only to four-sided regions.) For more information, see What is mapped meshing?, and When can Abaqus/CAE apply mapped meshing?. When mapped meshing is used, Abaqus/CAE makes minor adjustments to the mesh seeding. If you do not want the seeding to change, you can use mesh controls to prevent the use of mapped meshing. For more information, see Assigning mesh controls.
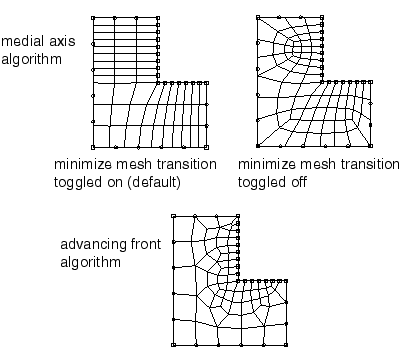
By default, Abaqus/CAE minimizes the mesh transition when it generates a free quadrilateral mesh using the medial axis algorithm. Minimizing the mesh transition results in a better mesh that is generated more quickly; however, the generated nodes deviate further from the mesh seeds. Figure 4 illustrates the same planar part instance meshed using the medial axis algorithm with and without minimizing the mesh transition and meshed using the advancing front algorithm.