How are precision and tolerance related? | ||
| ||
To successfully import a solid defined by trimmed surfaces or B-reps, the tolerance of the original file and the tolerance of Abaqus/CAE must match within an acceptable limit. If the tolerance of the original file is considerably looser than the tolerance of Abaqus/CAE, the import may fail because Abaqus/CAE cannot reconstruct the solid from the trimmed surfaces and B-rep information.
After you import a part into Abaqus/CAE, the healing process is designed to improve the part's accuracy. Abaqus/CAE tries to change neighboring entities so that their geometry matches exactly. Converting to a precise representation usually results in precise geometry. However, this can be a lengthy operation that increases the complexity of the imported part. As a result, subsequent processing and analysis of the part may be slower. Moreover, if the part contains many complex surfaces, converting to a precise representation is likely to fail. If possible, you should return to the CAD application that generated the original file and increase the precision.
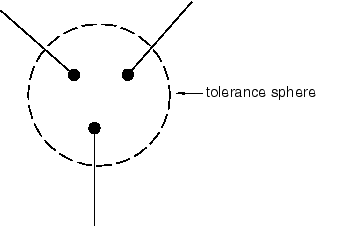
You can use the Query toolset in the Part module to highlight regions of an imported part that have geometry precision and validity errors. An imprecise vertex can be thought of as a vertex surrounded by an imaginary sphere, where the diameter of the sphere is equal to the local precision. When you heal a part, ACIS assumes that any point inside the imaginary sphere is coincident with the vertex, as shown in Figure 1.
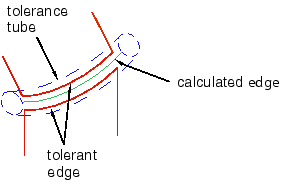
Similarly, an imprecise edge can be thought of as an edge surrounded by an imaginary tube, where the diameter of the tube is equal to the local precision. When you heal a part, ACIS assumes that any point inside the imaginary tube is lying on the edge, as shown in Figure 2.
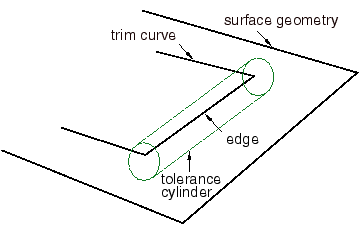
During the healing process ACIS also uses tolerance to determine if a trim curve is positioned on the underlying surface geometry, as shown in Figure 3.