How the position constraint methods differ | ||
| ||
-
Parallel face (three-dimensional instances only)
-
Face to face (three-dimensional instances only)
-
Parallel edge
-
Edge to edge
-
Coaxial (three-dimensional instances only)
-
Coincident point
-
Parallel coordinate systems
In general, applying a single position constraint is not sufficient to define the precise location of a movable instance. You must apply several position constraints—usually three for a three-dimensional assembly and two for a two-dimensional assembly—to position an instance in the desired location. Part and model instances can overlap as a result of applying position constraints; Abaqus/CAE does not prevent overclosure between edges, faces, or cells. Similarly, Abaqus/CAE does not prevent you from overconstraining instances or duplicating a constraint.
The definition of a constraint feature includes all the faces and edges that you originally selected. If you subsequently modify a part or move a part or model instance, Abaqus/CAE automatically recalculates the constraint based on your original selection of faces and edges. As a result, one or more instances may move after the assembly is regenerated. For example, different edges may become parallel. For more information on features, see Manipulating features in the Assembly module and The Feature Manipulation toolset.
The following position constraints are provided by the Assembly module:
- Parallel Face
-
A parallel face position constraint causes a selected face of the movable instance to become parallel with a selected face of the fixed instance. However, the position constraint does not specify the precise location of the movable instance, and the distance between the parallel faces is arbitrary. To apply a parallel face position constraint between two instances, you do the following:
-
Select the faces to be constrained to be parallel from the movable instance and the fixed instance, as shown in Figure 1.
Figure 1. Select the faces to become parallel.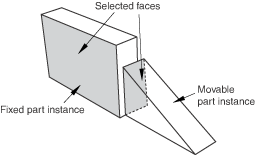
-
Abaqus/CAE displays arrows normal to the selected faces. You prescribe the orientation of the movable instance by selecting the direction of the arrow normal to its selected face. Figure 2 illustrates the result of applying the position constraint and the effect on the movable instance of reversing the direction of the arrow.
Figure 2. The result of applying a parallel face position constraint and the effect of changing the direction of the arrow normal to the selected face of the movable instance.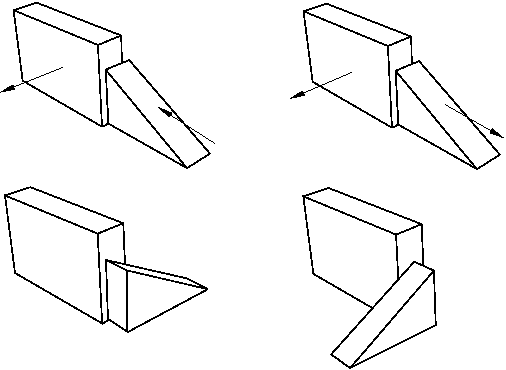
Abaqus/CAE rotates the movable instance until the two selected faces are parallel and the arrows are pointing in the same direction.
The faces you select from the movable and fixed instances must be planar. The parallel face position constraint can be applied only to three-dimensional instances.
-
- Face to Face
-
A face-to-face position constraint is similar to a parallel face position constraint except that you define the clearance between the parallel faces. The clearance is measured between the two selected faces, positive along the normal to the fixed instance. Other than this clearance, the precise location of the movable instance is not constrained. Assuming that you selected the same two faces shown in Figure 1, the effect of applying a face-to-face constraint is shown in Figure 3. Figure 3 also illustrates the effect on the movable instance of reversing the direction of the arrow normal to its selected face.
Figure 3. The result of applying a face-to-face constraint and the effect of changing the direction of the arrow normal to the selected face of the movable instance.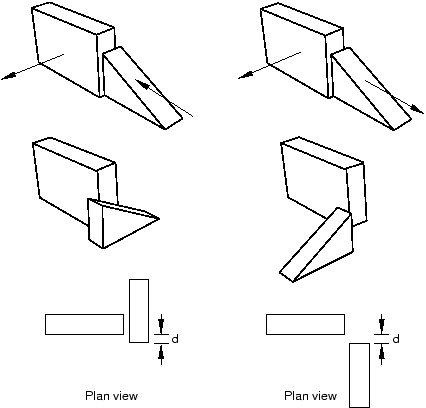
Abaqus/CAE rotates the movable instance until the two selected faces are parallel and the arrows point in the same direction. In addition, the movable instance is translated to satisfy the clearance specified. The faces you select from the movable and fixed instances must be planar. The face-to-face position constraint can be applied only to three-dimensional instances.
- Parallel Edge
-
A parallel edge position constraint causes a selected edge of the movable instance to become parallel with a selected edge of the fixed instance. However, the position constraint does not specify the precise location of the movable instance, and the distance between the parallel edges is arbitrary. To apply a parallel edge position constraint between two instances, you do the following:
-
Select the edges to be constrained to be parallel from the movable and fixed instance, as shown in Figure 4.
Figure 4. Select the edges to become parallel.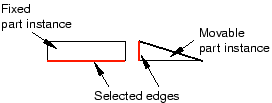
-
Abaqus/CAE displays arrows along the selected edges. You prescribe the orientation of the movable instance by selecting the direction of the arrow along its selected edge. Figure 5 illustrates the result of applying the position constraint and the effect on the movable instance of reversing the direction of the arrow.
Figure 5. The result of applying a parallel edge constraint and the effect of changing the direction of the arrow along the selected edge of the movable instance.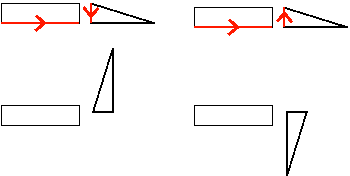
Abaqus/CAE rotates the movable instance until the two selected edges are parallel and the arrows point in the same direction.
The edges you select from the movable and fixed instances must be straight. You can select an edge from an instance, or you can select a datum axis or one of the axes of a datum coordinate system. The parallel edge position constraint can be applied only to two-dimensional and three-dimensional instances. It has no effect on axisymmetric instances.
-
- Edge to Edge
-
An edge-to-edge position constraint is similar to a parallel edge position constraint except that the clearance between the parallel edges is defined by the constraint. Assuming that you selected the same two edges shown in Figure 4, the effect of applying an edge-to edge position constraint to a two-dimensional assembly is shown in Figure 6. Figure 6 also illustrates the effect on the movable instance of reversing the direction of the arrow along its selected edge.
Figure 6. The result of applying an edge-to-edge constraint and the effect of changing the direction of the arrow along the selected edge of the movable instance.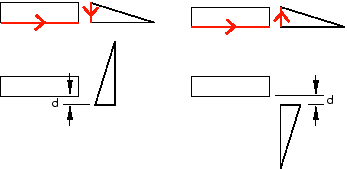
The modeling space of the assembly determines the behavior of Abaqus/CAE after you apply an edge-to-edge position constraint.
-
If the assembly is three-dimensional, Abaqus/CAE positions the movable instance so that the edges are coincident.
-
If the assembly is two-dimensional, you can specify the clearance between the selected edges. The clearance is measured between the two selected edges, positive along the normal to the fixed instance.
Other than this behavior, the precise location of the movable instance is not constrained. The edge-to-edge position constraint can be applied to two-dimensional, three-dimensional, and axisymmetric instances; however, axisymmetric instances can move only parallel to the axis of revolution.
-
- Coaxial
-
A coaxial position constraint causes a selected cylindrical or conical face of the movable instance to become coaxial with a selected cylindrical or conical face of the fixed instance. However, the coaxial position constraint does not constrain the precise location of the movable instance. To apply a coaxial position constraint between two instances, you do the following:
-
Select the cylindrical or conical faces to be constrained to be coaxial from the movable and fixed instance, as shown in Figure 7.
Figure 7. Select the faces to become coaxial.
-
Abaqus/CAE displays arrows along the axis of revolution of the selected instances. You prescribe the orientation of the movable instance by selecting the direction of the arrow along its axis of revolution. Figure 8 illustrates the result of applying the coaxial position constraint.
Figure 8. The effect of applying a coaxial constraint.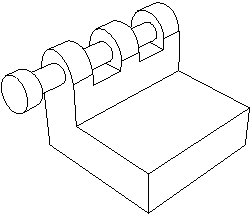
Abaqus/CAE rotates and translates the movable instance until the two selected faces are coaxial and the arrows are pointing in the same direction. The coaxial position constraint can be applied only to three-dimensional instances.
-
- Coincident Point
-
A coincident point constraint causes a selected point on the movable instance to coincide with a selected point on the fixed instance. However, the coincident point constraint does not constrain the orientation of the movable instance. The orientation of the movable instance does not change after the constraint is applied, as shown in Figure 9. For detailed instructions, see Constraining two instances with coincident points.
Figure 9. The effect of applying a coincident point constraint.
- Parallel CSYS
-
A parallel coordinate systems constraint causes the axes of a datum coordinate system on the movable instance to become parallel with the axes of a datum coordinate system on the fixed instance. However, the parallel coordinate systems constraint does not specify the precise location of the movable instance. Figure 10 illustrates the effect of applying a parallel coordinate systems constraint and a concident point constraint to two instances.
Figure 10. The effect of applying parallel coordinate systems and coincident point constraints.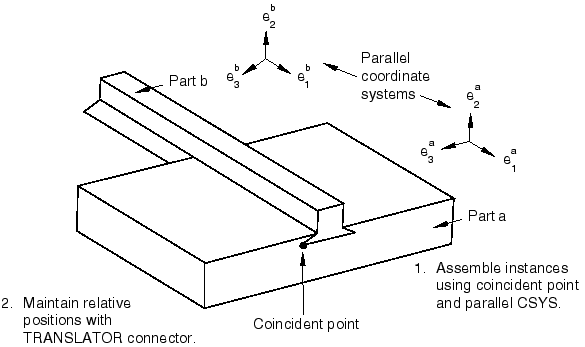
The coordinate systems can be either rectangular (X-, Y-, and Z-axes), cylindrical (R-, -, and Z-axes), or spherical (R-, -, and -axes). For detailed instructions, see Constraining two instances with parallel coordinate systems.
You can use datums to position part and model instances. When you are prompted to select a face, you can also select a datum plane. When you are prompted to select an edge, you can also select a datum axis or one of the axes of a datum coordinate system. You can select a datum that you created in the Part module because the datum is associated with an instance of the part and moves with the part instance. However, if the position constraint uses a datum that you created in the Assembly module by selecting from a part instance (such as a face of a part instance), Abaqus/CAE changes its regeneration behavior and regenerates features in the order that you created them. For more information, see How are position constraints regenerated?. You cannot select a datum as the movable part instance if you created the datum in the Assembly module and it depends on more than one part instance; for example, a datum axis that runs through vertices of two part instances.