Finite deformation of an elastic-plastic granular material

This example develops the homogeneous, finite-strain inelastic response of a granular material subject to uniform extension or compression in plane strain. Results given by Carter et al. (1977) for these cases are used for comparison.

The following topics are discussed:

Problem description
Results and discussion
Input files
References
Figures

ProductsAbaqus/StandardAbaqus/Explicit

Problem description

The specimen is initially stress-free and is made of an elastic, perfectly plastic material. The elasticity is linear, with a Young's modulus of 30 MPa and a Poisson's ratio of 0.3. Carter et al. assume that the inelastic response is governed by a Mohr-Coulomb failure surface, defined by the friction angle of the Coulomb line ( $ϕ = $ 30°) and the material's cohesion (c). They also assume that the cohesion is twice the Young's modulus for the extension test and 10% of the Young's modulus in the compression test. The above problem is solved using the Mohr-Coulomb plasticity model in Abaqus with the friction angle and the dilation angle equal to 30°. However, note that this Abaqus Mohr-Coulomb model is not identical to the classical Mohr-Coulomb model used by Carter because it uses a smooth flow potential.

An alternative solution is to use the associated linear Drucker-Prager surface in place of the Mohr-Coulomb surface. In this case it is necessary to relate $ϕ$ and c to the material constants $β$ and $σ_{c}^{0} = d / (1 - \frac{1}{3} \tan β)$ that are used in the Drucker-Prager model. Matching procedures are discussed in Extended Drucker-Prager models. In this case we select a match appropriate for plane strain conditions:

\tan β = \frac{3 \sqrt{3} \tan ϕ}{\sqrt{9 + 12 \tan^{2} ϕ}}

d = \frac{3 \sqrt{3} c}{\sqrt{9 + 12 \tan^{2} ϕ}} .

The first equation gives $β = $ 40°. Using the assumptions of Carter et al., the second equation gives d as 86.47 MPa ( $σ_{c}^{0}$ = 120 MPa) for the extension case and d as 4.323 MPa ( $σ_{c}^{0}$ = 6 MPa) for the compression case.

Uniform extension or compression of the soil sample is specified by displacement boundary conditions since the load-displacement response will be unstable for the extension case.

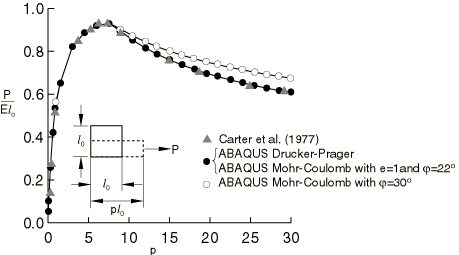
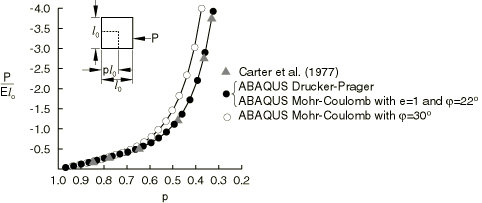
Results and discussion

The results are shown in Figure 1 for extension and in Figure 2 for compression. The solutions for Abaqus/Standard and Abaqus/Explicit are the same. The Drucker-Prager solutions agree well with the results given by Carter et al.; this is to be expected since the Drucker-Prager parameters are matched to the classical Mohr-Coulomb parameters under plane strain conditions. The differences between the Abaqus Mohr-Coulomb solutions and Carter's solutions are due to the fact that the Abaqus Mohr-Coulomb model uses a different flow potential. The Abaqus Mohr-Coulomb model uses a smooth flow potential that matches the classical Mohr-Coulomb surface only at the triaxial extension and compression meridians (not in plane strain).

However, one can also obtain Abaqus Mohr-Coulomb solutions that match Carter's plane strain solutions exactly. As discussed earlier, the classical Mohr-Coloumb model can be matched under plane strain conditions to an associated linear Drucker-Prager model with the flow potential

G = q - p \tan β .

This match implies that under plane strain conditions the flow direction of the classical Mohr-Coulomb model can be alternatively calculated by the corresponding flow direction of the Drucker-Prager model with the dilation angle $β$ as computed before. Therefore, we can match the flow potential of the Abaqus Mohr-Coulomb model to that of the Drucker-Prager model. Matching between these two forms of flow potential assumes $e = $ 1 and results in

\tan ψ = R_{m c} (\frac{π}{3}, ϕ) \tan β = \frac{3 - \sin ϕ}{6 \cos ϕ} \tan β,

which gives $ψ = $ 22° in the Abaqus Mohr-Coulomb model. These Abaqus Mohr-Coulomb solutions are shown in Figure 1 and Figure 2 and match Carter's solutions exactly.

Input files

Abaqus/Standard input files

deformgranularmat_mc3030.inp: Extension case with the Mohr-Coulomb plasticity model ( $ϕ = $ 30° and $ψ = $ 30°) and CPE4 elements.
deformgranularmat_dp.inp: Extension and compression cases with the linear Drucker-Prager plasticity model and CPE4 elements.
deformgranularmat_cpe4i_dp.inp: Extension case with the linear Drucker-Prager plasticity model and CPE4I incompatible mode elements.
deformgranularmat_mc3030_comp.inp: Compression case with the Mohr-Coulomb plasticity model ( $ϕ = $ 30° and $ψ = $ 30°) and CPE4 elements.
deformgranularmat_dp_comp.inp: Compression case with the linear Drucker-Prager plasticity model and CPE4 elements.
deformgranularmat_mc3022.inp: Extension case with the Mohr-Coulomb plasticity model ( $ϕ = $ 30° and $ψ = $ 22°) and CPE4 elements.
deformgranularmat_mc3022_comp.inp: Compression case with the Mohr-Coulomb plasticity model ( $ϕ = $ 30° and $ψ = $ 22°) and CPE4 elements.

Abaqus/Explicit input files

granular.inp: Extension and compression cases with the linear Drucker-Prager plasticity model and CPE4R elements.
deformgranularmat_mc3030_xpl.inp: Extension case with the Mohr-Coulomb plasticity model ( $ϕ = $ 30° and $ψ = $ 30°) and CPE4R elements.
deformgranularmat_mc3030_comp_xpl.inp: Compression case with the Mohr-Coulomb plasticity model ( $ϕ = $ 30° and $ψ = $ 30°) and CPE4R elements.
deformgranularmat_mc3022_xpl.inp: Extension case with the Mohr-Coulomb plasticity model ( $ϕ = $ 30° and $ψ = $ 22°) and CPE4R elements.
deformgranularmat_mc3022_comp_xpl.inp: Compression case with the Mohr-Coulomb plasticity model ( $ϕ = $ 30° and $ψ = $ 22°) and CPE4R elements.

References

Carter, J. P., J. R. Booker, and E. H. Davis, “Finite Deformation of an Elasto-Plastic Soil,” International Journal for Numerical and Analytical Methods in Geomechanics, vol. 1, pp. 25–43, 1977.

Figures

Figure 1. Load-displacement results for uniform extension.

Figure 2. Load-displacement results for uniform compression.