Minimizing the Volume of the Crane Hook Model (Tosca ANSA® environment)

Depending on the used solver, the analysis can be performed in one or two solver runs.

Related Topics
About Checking the Quality of the Optimization Result

  1. Choose a TOPOLOGY_OPTIMIZATION_SENSITIVITY task and create the model link.

  2. Create the design area of all elements and fix the frozen_elements element group.

  3. Define a demold restriction on all elements using a middle plane through the point with coordinates 0, 0, -20 and the global positive z-axis as pull direction.

  4. Set up the objective function to minimize the crane hook volume.

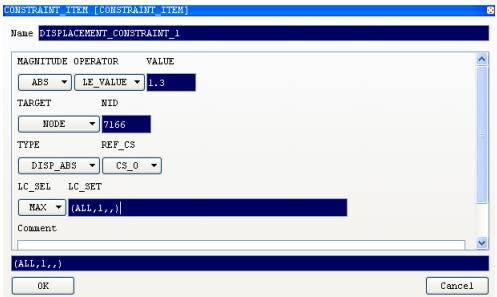
  5. To define a displacement constraint, select in the task manager PRE_PROCESSING | CONSTRAINTS | NEW | DISPLACEMENT_CONSTRAINT.

  6. In the CONSTRAINT item, switch the MAGNITUDE to ABS and enter the maximal value for the displacement in 1.3. Switch the TARGET to NODE and specify the node number 7166. Specify the load case number 1 for this constraint:



  7. Create an identical displacement constraint for load case number 2.

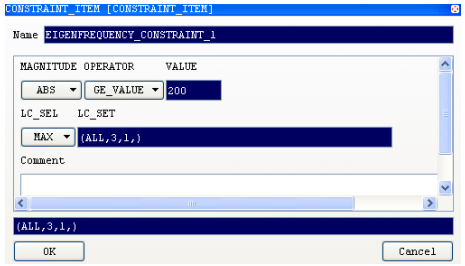
  8. To define a displacement constraint, select in the task manager PRE_PROCESSING | CONSTRAINTS | NEW | EIGENFREQUENCY_CONSTRAINT.

  9. In the CONSTRAINT item, switch the MAGNITUDE to ABS, select a GE_VALUE to and enter the minimum value for the first eigenfrequency, 200. Specify the load case number 3 and additionally the substep number 1 for this constraint. In this case the selected substep number will refer to the eigenfrequency with the same order number:



The optimization result looks as follows:

The convergence plot for the Objective Function is as follows:



The convergence plot for Frequency Constraint is as follows: