Multiaxial cyclic hardening

These criteria differ from the strain-based multiaxial fatigue criteria already described in that they require stresses in addition to strain amplitudes. This requires a method of calculating true cyclic elastic-plastic stresses at any point in a complex strain history under multiaxial cyclic strain conditions.

For uniaxial stress, if yielding occurs, the stress developed for any strain is path dependent. This means that the stress is not determined only by the applied strain, but by the time history of applied strains. This is illustrated in Figure 7.43(a) which shows a simple strain excursion, and the stress associated with it.

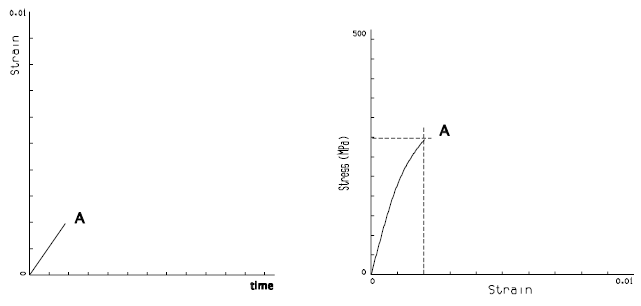
Figure 7.43(b) shows the same applied strain, preceded by a larger tensile strain excursion.

In each case the final strain excursion is the same, but the associated peak stress is quite different. This sequence effect, or path dependency, is allowed for in uniaxial analysis, and must be included in any proposed multi-axial analysis.

Considering again the uniaxial stress condition, with a sequence of applied strains. The largest strains are associated with the largest hysteresis loop (the outside loop). Figure 7.44 also shows the stressstrain response for the two smaller strain excursions AA and BB and it can be seen that they differ in two aspects: the amount of elastic behaviour, and the shapes of the stress-strain curves.

The amount of elastic behaviour is determined by how close the strain is to the yield point for the curve. In the case illustrated, this is how close the strain is to the outside loop. In general it is determined by how close the strain is to the previous position of the yield point.

It can also be seen from Figure 7.44 that the stress-strain curve for BB is much flatter than that for AA, BB is closer to the maximum strain produced by the strain history. If the maximum strain is a limit, then the shape of the stress-strain curve is determined by its distance from the limit. For uniaxial conditions there are two limit points, which are the maximum and minimum points in the signal, and correspond to the outside loop. For a strain excursion such as AA or BB, the shape of an up-going stress-strain curve is determined by its distance from the maximum limit, and the shape of a down-going stress-strain curve is determined by its distance from the minimum limit.

These concepts of path dependency and of stress-strain curves whose shape is governed by their proximity to the limit conditions need to be translated into their multiaxial equivalents.

From Section 7.2.2, for elastic behaviour:

${\epsilon }_x=\frac{1}{E}[{\sigma }_x-v({\sigma }_y+{\sigma }_z\left)\right]$

${\epsilon }_y=\frac{1}{E}[{\sigma }_y-v({\sigma }_z+{\sigma }_x\left)\right]$

${\epsilon }_z=\frac{1}{E}[{\sigma }_z-v({\sigma }_x+{\sigma }_y\left)\right]$

${\gamma }_{yz}=\frac{{\tau }_{yz}}{2G}$

${\gamma }_{zx}=\frac{{\tau }_{zx}}{2G}$

${\gamma }_{xy}=\frac{{\tau }_{xy}}{2G}$

The hydrostatic stress is ${\sigma }_m=\frac{{\sigma }_x+{\sigma }_y+{\sigma }_z}{3}$

and the equations can be re-written as

${\epsilon }_x=\frac{1}{2G}({\sigma }_x-{\sigma }_m)+\frac{(1-2n)}{E}{\sigma }_m$

${\epsilon }_y=\frac{1}{2G}({\sigma }_y-{\sigma }_m)+\frac{(1-2n)}{E}{\sigma }_m$

${\epsilon }_z=\frac{1}{2G}({\sigma }_z-{\sigma }_m)+\frac{(1-2n)}{E}{\sigma }_m$

${\gamma }_{yz}=\frac{{\tau }_{yz}}{2G}$

${\gamma }_{zx}=\frac{{\tau }_{zx}}{2G}$

${\gamma }_{xy}=\frac{{\tau }_{xy}}{2G}$

The terms $({\sigma }_x-{\sigma }_m)$ etc. are the deviatoric stresses $S_x$ etc. and as the deviatoric shear stresses and strains are equal to the total shear stresses and strains, the complete elastic stress-strain relationships can be written simply as

${{\epsilon }^e}_{ij}=\frac{S_{ij}}{2G}+\frac{(1-2n)}{E}{\sigma }_m$

For the plastic component of strain, the Reuss flow rule assumes that the plastic component of strain increment is proportional to the deviatoric and shear stresses:

$\frac{{{d\epsilon }^p}_x}{S_x}=\frac{{{d\epsilon }^p}_y}{S_y}=\frac{{{d\epsilon }^p}_z}{S_z}=\frac{{{d\gamma }^p}_{xy}}{S_{xy}}=\frac{{{d\gamma }^p}_{yz}}{S_{yz}}=\frac{{{d\gamma }^p}_{xz}}{S_{xz}}=d\lambda$

or $\frac{{{d\epsilon }^p}_{ij}}{S_{ij}}=d\lambda$ or ${{d\epsilon }^p}_{ij}=d\lambda S_{ij}$

This equation can only be used to calculate increments of plastic strain, because the factor dλ which relates strain to deviatoric stress will change with stress. Total plastic strain is obtained by integrating the equation along the strain path.